【题目】我国古代数学著作《九章算术》中有这样一个问题:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适于岸齐,问水深、葭长各几何?”这道题的意思是说:“有一个边长为10尺的正方形水池,在水池的正中央长着一根芦苇,芦苇露出水面1尺,若将芦苇拉到水池一边的中点处,芦苇的顶端恰好到达池边的水面,问水的深度与这根芦苇的长度分别是多少?若设水的深度为x尺,则可以得到方程_____.

参考答案:
【答案】x2+52=(x+1)2.
【解析】
我们可以将其转化为数学几何图形,如图所示,根据题意,可知EB'的长为10尺,则B'C=5尺,设出AB=AB'=x尺,表示出水深AC,根据勾股定理建立方程即可.
依题意画出图形,
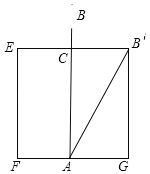
设芦苇长AB=AB′=x尺,则水深AC=(x﹣1)尺,因为B'E=10尺,所以B'C=5尺,
在Rt△AB'C中,∵CB′2+AC2=AB′2
∴52+(x﹣1)2=x2,
故答案为:x2+52=(x+1)2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 是原点,
是原点, (0,3),
(0,3), (4,0),
(4,0), 是
是 的角平分线.
的角平分线.
(1)确定
 所在直线的函数表达式;
所在直线的函数表达式;(2)在线段
 上是否有一点
上是否有一点 ,使点
,使点 到
到 轴和
轴和 轴的距离相等,若存在,求出点
轴的距离相等,若存在,求出点 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;(3)在线段
 上是否有一点
上是否有一点 ,使
,使 是等腰三角形,若存在,直接写出 点
是等腰三角形,若存在,直接写出 点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】2002年国际数学家大会在北京召开,大会选用了赵爽弦图作为会标的中心图案.如图,由四个全等的直角三角形与一个小正方形拼成一个大正方形.如果大正方形的面积是25,直角三角形较长的直角边长是a,较短的直角边长是b,且(a+b)2的值为49,那么小正方形的面积是( )

A.2B.0.5C.13D.1
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线
 在平面直角坐标系中的位置如图所示,则下列结论:
在平面直角坐标系中的位置如图所示,则下列结论:①
 ;②
;② ;③
;③ ;④
;④ .
.其中,正确的结论的个数是( )

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种商品的成本是
 元,试销阶段每件商品的售价
元,试销阶段每件商品的售价 (元)与产品的销售量
(元)与产品的销售量 (件)满足当
(件)满足当 时,
时, ,当
,当 时,
时, ,且
,且 是
是 的一次函数,为了获得最大利润
的一次函数,为了获得最大利润 (元),每件产品的销售价应定为( )
(元),每件产品的销售价应定为( )A. 160元 B. 180元 C. 140元 D. 200元
-
科目: 来源: 题型:
查看答案和解析>>【题目】若所求的二次函数图象与抛物线
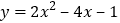 有相同的顶点,并且在对称轴的左侧,
有相同的顶点,并且在对称轴的左侧,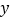 随
随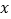 的增大而增大,在对称轴的右侧,
的增大而增大,在对称轴的右侧,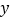 随
随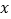 的增大而减小,则所求二次函数的解析式为( )
的增大而减小,则所求二次函数的解析式为( )A.
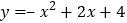
B.

C.
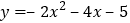
D.
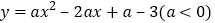
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:把Rt△ABC和Rt△DEF按如图1摆放(点C与点E重合),点B、C(E)、F在同一条直线上,∠ACB=∠EDF=90°,∠DEF=45°,AC=8cm,BC=6cm,EF=9cm,如图2,△DEF从图1的位置出发,以1cm/s的速度沿CB向△ABC匀速移动,在△DEF移动的同时,点P从△ABC的顶点B出发,以2cm/s的速度沿BA向点A匀速移动.当△DEF的顶点D移动到AC边上时,△DEF停止移动,点P也随之停止移动.DE与AC相交于点Q,连接PQ,设移动时间为t(s)(0<t<4.5).解答下列问题:
(1)用含t的代数式表示线段AP= ;
(2)当t为何值时,点E在∠A的平分线上?
(3)当t为何值时,点A在线段PQ的垂直平分线上?
(4)连接PE,当t=1(s)时,求四边形APEC的面积.

相关试题

