搜索
【题目】如图，在
中，
，
的垂直平分线交于点
，交
于点
．
（1）若
，求
的长；
（2）若
，求证：
是等腰三角形．
参考答案：
【答案】（1）
；（2）见解析.
【解析】
（1）根据线段垂直平分线的性质可得EA＝EB，即
，结合
可求出
，进而得到CE的长；
（2）根据三角形内角和定理和等腰三角形的性质求出∠C＝72°，根据线段垂直平分线的性质可得EA＝EB，求出∠EBA＝∠A＝36°，然后利用三角形外角的性质得到∠BEC＝72°即可得出结论.
解：（1）∵DE是AB的垂直平分线，
∴EA＝EB，
∴，
∵
，
∴，
∴；
（2）∵
，
，
∴∠ABC＝∠C＝
，
∵DE是AB的垂直平分线，
∴EA＝EB，
∴∠EBA＝∠A＝36°，
∴∠BEC＝∠EBA＋∠A＝72°，
∴∠C＝∠BEC，
∴BC＝BE，即
是等腰三角形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某歌星演唱会票价如下：甲种票每张200元，乙种票每张100元．工会小组准备了1000元，全部用来买票，且每种至少买一张．
(1)共有多少种购票方案？列举出所有可能结果；
(2)如果从上述方案中任意选中一种方案购票，求恰好买到7张门票的概率．
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知二次函数
，点
在该函数的图象上，点到
轴、
轴的距离分别为
、
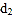．设
，下列结论中：①
没有最大值；②没有最小值；③
时，随的增大而增大；④满足
的点有四个．其中正确结论的个数有（ ）A.
个 B. 
个 C. 
个 D. 
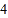个 -
科目： 来源： 题型：
查看答案和解析>>【题目】某校对全校3000名学生本学期参加艺术学习活动的情况进行评价，其中甲班学生本学期参观美术馆的次数以及艺术评价等级和艺术赋分的统计情况，如下表所示：
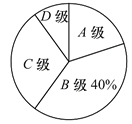
图（1） 图（2）
(1)甲班学生总数为______________人，表格中
的值为_____________；(2)甲班学生艺术赋分的平均分是______________分；
(3)根据统计结果，估计全校3000名学生艺术评价等级为
级的人数是多少？ -
科目： 来源： 题型：
查看答案和解析>>【题目】某旅行团去景点游览，共有成人和儿童20人，且旅行团中儿童人数多于成人．景点规定：成人票40元/张，儿童票20元/张．
（1）若20人买门票共花费560元，求成人和儿童各多少人？
（2）景区推出“庆元旦”优惠方案，具体方案为：
方案一：购买一张成人票免一张儿童票费用；
方案二：成人票和儿童票都打八折优惠；
设：旅行团中有成人a人，旅行团的门票总费用为W元．
①方案一：
_____________________；方案二：
____________________；②试随着a的变化，哪种方案更优惠？
-
科目： 来源： 题型：
查看答案和解析>>【题目】二次函数
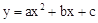（a、b、c为常数且a≠0）中的x与y的部分对应值如下表：x
﹣3
﹣2
﹣1
0
1
2
3
4
5
y
12
5
0
﹣3
﹣4
﹣3
0
5
12
给出了结论：
（1）二次函数
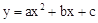有最小值，最小值为﹣3；（2）当
时，y＜0；（3）二次函数
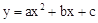的图象与x轴有两个交点，且它们分别在y轴两侧．则其中正确结论的个数是
A. 3 B. 2 C. 1 D. 0
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在
中，
是原点，
（0，3），
（4，0），
是的角平分线．
（1）确定
所在直线的函数表达式；（2）在线段
上是否有一点
，使点到
轴和
轴的距离相等，若存在,求出点的坐标；若不存在，请说明理由；（3）在线段
上是否有一点
，使
是等腰三角形，若存在，直接写出 点的坐标；若不存在，请说明理由．
相关试题
