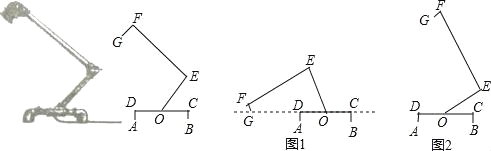
【题目】小华在“科技创新大赛”中制作了一个创意台灯作品,现忽略支管的粗细,得到它的侧面简化结构图如图所示.已知台灯底部支架CD平行于水平面,FE⊥OE,GF⊥EF,台灯上部可绕点O旋转,OE=20cm,EF=20![]() cm.
cm.
(1)如图1,若将台灯上部绕点O逆时针转动,当点G落在直线CD上时,测量得∠EOG=65°,求FG的长度(结果精确到0.1cm);
(2)将台灯由图1位置旋转到图2的位置,若此时F,O两点所在的直线恰好与CD垂直,求点F在旋转过程中所形成的弧的长度.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14,![]() ≈1.73,可使用科学计算器)
≈1.73,可使用科学计算器)
参考答案:
【答案】(1)FG的长度约为3.8cm.
(2)![]() cm
cm
【解析】
试题分析:(1)作GM⊥OE可得矩形EFGM,设FG=xcm,可知EF=GM=20![]() cm,OM=(20﹣x)cm,根据tan∠EOG=
cm,OM=(20﹣x)cm,根据tan∠EOG= ![]() 列方程可求得x的值;
列方程可求得x的值;
(2)RT△EFO中求出OF的长及∠EOF的度数,由∠EOG度数可得旋转角∠FOF′度数,根据弧长公式计算可得.
试题解析:(1)如图,作GM⊥OE于点M,

∵FE⊥OE,GF⊥EF,
∴四边形EFGM为矩形,
设FG=xcm,
∴EF=GM=20![]() cm,FG=EM=xcm,
cm,FG=EM=xcm,
∵OE=20cm,
∴OM=(20﹣x)cm,
在RT△OGM中,
∵∠EOG=65°,
∴tan∠EOG=![]() ,即
,即![]() =tan65°,
=tan65°,
解得:x≈3.8cm;
故FG的长度约为3.8cm.
(2)连接OF,
在RT△EFO中,∵EF=20![]() ,EO=20,
,EO=20,
∴FO=![]() =40,tan∠EOF=
=40,tan∠EOF= ![]() =
=![]() =
=![]() ,
,
∴∠EOF=60°,
∴∠FOG=∠EOG﹣∠EOF=5°,
又∵∠GOF′=90°,
∴∠FOF′=85°,
∴点F在旋转过程中所形成的弧的长度为:![]() =
=![]() cm.
cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,O为直线AB上一点,∠DOE=90°,OD是∠AOC的角平分线,若∠AOC=70°.
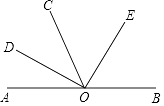
(1)求∠BOD的度数.
(2)试判断OE是否平分∠BOC,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】当x=3时,代数式ax2-3x-4的值为5,则字母a的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个多项式A减去多项式2x2﹣3x+5,糊涂同学将减号抄成了加号,运算结果为﹣x2﹣3x+4,求原题的正确结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:x3-64x=________.
-
科目: 来源: 题型:
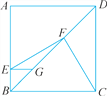
查看答案和解析>>【题目】如图,在正方形ABCD中,点E,G分别在边AB,对角线BD上,EG∥AD,F为GD的中点,连结FC,请利用勾股定理的逆定理,证明EF⊥FC.
-
科目: 来源: 题型:
查看答案和解析>>【题目】安宁市的一种绿色蔬菜,若在市场上直接销售,每吨利润为1000元,若经粗加工后销售,每吨利润可达4500元;若经精加工后销售每吨获利7500元.当地一家农产品企业收购这种蔬菜140吨,该企业加工厂的生产能力是:如果对蔬菜进行粗加工,每天可以加工16吨,如果进行精加工,每天可加工6吨,但两种加工方式不能同时进行,受季节条件限制,企业必须在15天的时间将这批蔬菜全部销售或加工完毕,企业研制了四种可行方案: 方案一:全部直接销售;
方案二:全部进行粗加工;
方案三:尽可能多地进行精加工,没有来得及进行精加工的直接销售;
方案四:将一部分进行精加工,其余的进行粗加工,并恰好15天完成.
请通过计算以上四个方案的利润,帮助企业选择一个最佳方案使所获利润最多?
相关试题

