【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

参考答案:
【答案】 16 ![]()
【解析】∵如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,
∴EF、FG、EG为三角形中位线,
∴EF=![]() BC,EG=
BC,EG=![]() AC,FG=
AC,FG=![]() AB,
AB,
∴EF+FG+EG=![]() (BC+AC+AB),即△EFG的周长是△ABC周长的一半,
(BC+AC+AB),即△EFG的周长是△ABC周长的一半,
同理,△A′B′C′的周长是△EFG的周长的一半,即△A′B′C′的周长为![]() ×64=16,
×64=16,
以此类推,第n个小三角形的周长是第一个三角形周长的64×(![]() )n-1,
)n-1,
故答案为:16,64×(![]() )n-1.
)n-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)从图中可知,小明家离体育馆 米,父子俩在出发后 分钟相遇.
(2)求出父亲与小明相遇时距离体育馆还有多远?
(3)小明能否在比赛开始之前赶回体育馆?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
发言次数n
A
0≤n<3
B
3≤n<6
C
6≤n<9
D
9≤n<12
E
12≤n<15
F
15≤n<18
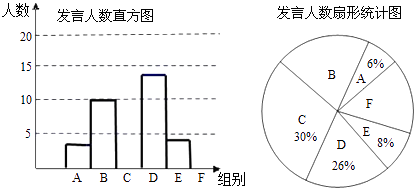
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:∠1= °,∠2= °;
(2)现把三角板绕B点逆时针旋转n°.
①如图2,当0<n<90,且点C恰好落在DG边上时,求∠1、∠2的度数(结果用含n的代数式表示);
②当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,直接写出所有n的值和对应的那两条垂线;如果不存在,说明理由.
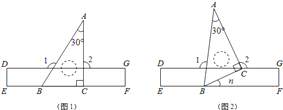
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD是矩形,E是BD上的一点,∠BAE=∠BCE,∠AED=∠CED,点G是BC、AE延长线的交点,AG与CD相交于点F.

(1)求证:四边形ABCD是正方形;
(2)当AE=2EF时,判断FG与EF有何数量关系?并证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
 的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1 , M2 , M3…,Mn , 则
的图象,当x取1,2,3,…,n时,对应在反比例图象上的点分别为M1 , M2 , M3…,Mn , 则  = .
= . 
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:△ABC的中线BD、CE交于点O,F、G分别是OB、OC的中点.求证:四边形DEFG是平行四边形.
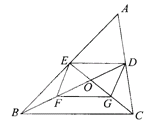
相关试题

