【题目】来自中国、美国、立陶宛、加拿大的四国青年男篮巅峰争霸赛于2014年3月25日-27日在我县体育馆举行。小明来到体育馆看球赛,进场时,发现门票还在家里,此时离比赛开始还有25分钟,于是立即步行回家取票.同时,他父亲从家里出发骑自行车以他3倍的速度给他送票,两人在途中相遇,相遇后小明立即坐父亲的自行车赶回体育馆.如图中线段AB、OB分别表示父、子俩送票、取票过程中,离体育馆的路程S(米)与所用时间t(分钟)之间的图象,结合图象解答下列问题(假设骑自行车和步行的速度始终保持不变):
(1)从图中可知,小明家离体育馆 米,父子俩在出发后 分钟相遇.
(2)求出父亲与小明相遇时距离体育馆还有多远?
(3)小明能否在比赛开始之前赶回体育馆?

参考答案:
【答案】(1)3600,15;(2) 900米 (3) 小明能在比赛开始之前赶回体育馆.
【解析】分析:(1)观察图象得到小明家离体育馆有3600米,小明到相遇地点时用了15分钟,则得到父子俩在出发后15分钟相遇;
(2)设小明的速度为x米/分,则他父亲的速度为3x米/分,利用父子俩在出发后15分钟相遇得到15x+3x15=3600,解得x=60米/分,则父亲与小明相遇时距离体育馆还有15x=900米;
(3)由(2)得到从B点到O点的速度为3x=180米/秒,则从B点到O点的所需时间=![]() =5(分),得到小明取票回到体育馆用了15+5=20分钟,小于25分钟,可判断小明能在比赛开始之前赶回体育馆.
=5(分),得到小明取票回到体育馆用了15+5=20分钟,小于25分钟,可判断小明能在比赛开始之前赶回体育馆.
详解:(1)∵O点与A点相距3600米,∴小明家离体育馆有3600米.
∵从点O点到点B用了15分钟,∴父子俩在出发后15分钟相遇;
(2)设小明的速度为x米/分,则他父亲的速度为3x米/分,根据题意得:
15x+3x15=3600,
解得:x=60米/分,∴15x=15×60=900(米)
即父亲与小明相遇时距离体育馆还有900米;
(3)∵从B点到O点的速度为3x=180米/秒,∴从B点到O点的所需时间=![]() =5(分),而小明从体育馆到点B用了15分钟,∴小明从点O到点B,再从点B到点O需15分+5分=20分.
=5(分),而小明从体育馆到点B用了15分钟,∴小明从点O到点B,再从点B到点O需15分+5分=20分.
∵小明从体育馆出发取票时,离比赛开始还有25分钟,∴小明能在比赛开始之前赶回体育馆.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,
 的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
的周长为36,对角线AC,BD相交于点O,点E是CD的中点,BD=12,求△DOE的周长.
-
科目: 来源: 题型:
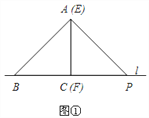
查看答案和解析>>【题目】如图①,将两块全等的三角板拼在一起,其中△ABC的边BC在直线l上,AC⊥BC且AC=BC;△EFP的边FP也在直线l上,边EF与边AC重合,EF⊥FP且EF=FP.
(1)在图①中,通过观察、测量,猜想直接写出AB与AP满足的数量关系和位置关系,不要说明理由;
(2)将三角板△EFP沿直线l向左平移到图②的位置时,EP交AC于点Q,连接AP、BQ.猜想写出BQ与AP满足的数量关系和位置关系,并说明理由.
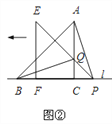
-
科目: 来源: 题型:
查看答案和解析>>【题目】探索规律:观察下面由※组成的图案和算式,解答问题:

1+3=22=4
1+3+5=32=9
1+3+5+7=42=16
1+3+5+7+9=52=25
(1)猜想1+3+5+7+9+…+29= = ;
(2)猜想1+3+5+7+9+…+(2n﹣1)+(2n+1)= = ;
(3)用上述规律计算:41+43+45+…+77+79.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校八年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,请结合图中相关数据回答下列问题:
发言次数n
A
0≤n<3
B
3≤n<6
C
6≤n<9
D
9≤n<12
E
12≤n<15
F
15≤n<18
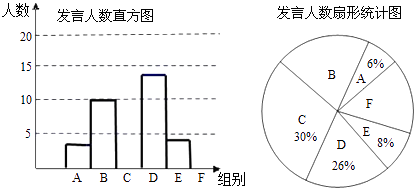
(1)求出样本容量,并补全直方图;
(2)该年级共有学生500人,请估计全年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰有1位女生,E组发言的学生中有2位男生.现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好是一男一女的概率. -
科目: 来源: 题型:
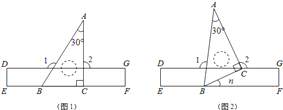
查看答案和解析>>【题目】如图1,把一块含30°的直角三角板ABC的BC边放置于长方形直尺DEFG的EF边上.
(1)填空:∠1= °,∠2= °;
(2)现把三角板绕B点逆时针旋转n°.
①如图2,当0<n<90,且点C恰好落在DG边上时,求∠1、∠2的度数(结果用含n的代数式表示);
②当0<n<360时,是否会存在三角板某一边所在的直线与直尺(有四条边)某一边所在的直线垂直?如果存在,直接写出所有n的值和对应的那两条垂线;如果不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC的周长为64,E、F、G分别为AB、AC、BC的中点,A′、B′、C′分别为EF、EG、GF的中点,△A′B′C′的周长为_________.如果△ABC、△EFG、△A′B′C′分别为第1个、第2个、第3个三角形,按照上述方法继续作三角形,那么第n个三角形的周长是__________________.

相关试题

