【题目】如图,长方形ABCD中,AB=4cm,BC=6cm,现有一动点P从A出发以2cm/秒的速度,沿矩形的边A﹣B﹣C运动,设点P运动的时间为t秒.
(1)当t为何值时,点P与点A的距离为5cm?
(2)当t为何值时,△APD是等腰三角形?
(3)当t为何值时,(2<t<5),以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边?
参考答案:
【答案】
(1)
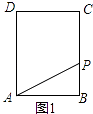
解:如图1,若点P在BC上,
∵在Rt△ABP中,AP=5,AB=4
∴BP=2t﹣4=3,
∴t= ![]() ;
;
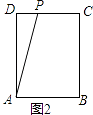
如图2,若点P在DC上,
则在Rt△ADP中,AP是斜边,
∵AD=6,
∴AP>6,
∴AP≠5.
综上所述,当t= ![]() 秒时,点P与点A的距离为5cm
秒时,点P与点A的距离为5cm
(2)
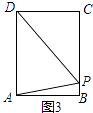
解:)当AD=DP时,如图3,PC=(10﹣2t)cm,CD=4cm,DP=6cm,
∵CD2+PC2=DP2,即42+(10﹣2t)2=62,解得t=5± ![]() ,即t1=5+
,即t1=5+ ![]() ,t2=5﹣
,t2=5﹣ ![]() ;
;
当DP=AP时,如图4,PC=PB=3cm,
∵AB=4cm,
∴AB+BP=4+3=7cm,
∴t= ![]() (秒);
(秒);
当AD=AP=6时,PB=2t﹣4,
∵AB2+BP2=AP2,即42+(2t﹣4)2=62,解得t=2+ ![]() 或t=2﹣
或t=2﹣ ![]() (舍去),
(舍去),
综上所述,当t=(5± ![]() )秒或t=
)秒或t= ![]() 秒时,△APD是等腰三角形
秒时,△APD是等腰三角形

(3)
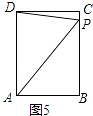
解:当2<t<5时,点P在BC边上,
∵BP=2t﹣4,CP=10﹣2t,
∴AP2=AB2+BP2=42+(2t﹣4)2
由题意,有AD2+CP2=AP2
∴62+(10﹣2t)2=42+(2t﹣4)2
∴t= ![]() <5,
<5,
∴t= ![]() .
.
答:当t= ![]() 秒时,以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边
秒时,以线段AD、CP、AP的长度为三边长的三角形是直角三角形,且AP是斜边
【解析】(1)分为两种情况:P在BC上,P在DC上,根据勾股定理得出关于t的方程,求出即可;(2)分AD=DP,DP=AP,AD=AP三种情况进行讨论;(3)求出BP=2t﹣4,CP=10﹣2t,根据AP2=AB2+BP2=42+(2t﹣4)2和AD2+CP2=AP2得出方程62+(10﹣2t)2=42+(2t﹣4)2 , 求出方程的解即可.
【考点精析】利用勾股定理的概念对题目进行判断即可得到答案,需要熟知直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在四边形ABCD中,∠ABC=∠ADC=90°,点E是AC的中点,连接BE、BD、DE.

(1)求证:△BED是等腰三角形;
(2)当∠BAD=°时,△BED是等腰直角三角形. -
科目: 来源: 题型:
查看答案和解析>>【题目】角平分线上的点到角两边的距离相等.这一性质在解决图形面积问题时有何妙用呢?阅读材料:已知,如图(1),在面积为S的△ABC中,BC=a,AC=b,AB=c,三条角平分线的交点O到三边的距离为r.连接OA、OB、OC,△ABC被划分为三个小三角形.
∵S=S△OBC+S△OAC+S△OAB= BCr+
BCr+  ACr+
ACr+  ABr=
ABr=  (a+b+c)r,∴r=
(a+b+c)r,∴r= 

(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图(2),各边长分别为AB=a,BC=b,CD=c,AD=d,求点O到四边的距离r;
(2)理解应用:如图(3),在四边形ABCD中,AB∥DC,AB=21,CD=11,AD=BC=13,对角线BD=20,点O1与O2分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为r1和r2 , 求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是方程ax﹣1=3的解,求a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市自来水公司为限制单位用水,每月只给某单位计划内用水300吨,计划内用水每吨收费3. 4元,超计划部分每吨按4. 6元收费.
(1)用代数式表示(所填结果需化简):
设用水量为
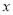 吨,当用水量小于等于300吨,需付款 元;当用水量大于300吨,需付款 元.
吨,当用水量小于等于300吨,需付款 元;当用水量大于300吨,需付款 元.(2)若某单位4月份缴纳水费1480元,则该单位用水多少吨?
(3)若某单位5、6月份共用水700吨(6月份用水量超过5月份),共交水费2560元,则该单位5、6月份各用水多少吨?
-
科目: 来源: 题型:
查看答案和解析>>【题目】定义一种运算“*”,其规则为a※b=a2﹣b2,则方程(x+2)*5=0的解为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若2x=5,2y=3,则22x+y=_____.
相关试题

