【题目】已知:如图,∠BAC的角平分线与BC的垂直平分线DG交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F.
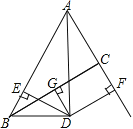
①求证:BE=CF;
②若AF=5,BC=6,求△ABC的周长.
参考答案:
【答案】(1)见解析;(2)16.
【解析】试题分析:①连接CD,根据垂直平分线性质可得BD=CD,可证Rt△BDE≌Rt△CDF,可得BE=CF;
②根据Rt△ADE≌Rt△ADF得出AE=AF解答即可.
试题解析:①证明:连结CD,
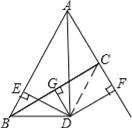
∵D在BC的中垂线上,
∴BD=CD,
∵DE⊥AB,DF⊥AC,AD平分∠BAC,
∴DE=DF,∠BED=∠DCF=90°,
在RT△BDE和RT△CDF中,DE=DF,BD=CD,
∴Rt△BDE≌Rt△CDF(HL),
∴BE=CF;
②解:由(HL)可得,Rt△ADE≌Rt△ADF,
∴AE=AF=5,
∴△ABC的周长=AB+BC+AC=(AE+BE)+BC+(AF﹣CF)=5+6+5=16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:等腰三角形两边长分别为9cm,5cm,则周长是( )
A. 19cm B. 23cm C. 19cm或23cm D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,正确的是
A. 三个角对应相等的两个三角形全等 B. 面积相等的两个三角形全等
C. 全等三角形的面积相等 D. 两边和其中一边的对角对应相等的两个三角形全等
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=6cm,∠B=∠C,BC=4cm,点D为AB的中点.
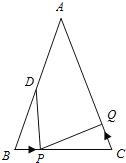
(1)如果点P在线段BC上以1cm/s的速度由点B向点C运动,同时,点Q在线段CA上由点C向点A运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿△ABC三边运动,则经过 后,点P与点Q第一次在△ABC的 边上相遇?(在横线上直接写出答案,不必书写解题过程)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是
A. 全等的两个图形一定成轴对称
B. 成轴对称的两个图形一定全等
C. 两个图形关于某直线对称,对称点一定在这直线的两旁
D. 两个图形关于某直线对称,对称点在这直线上
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明和几位同学做手的影子游戏时,发现对于同一物体,影子的大小与光源到物体的距离有关.因此,他们认为:可以借助物体的影子长度计算光源到物体的位置.于是,他们做了以下尝试.

(1)如图1,垂直于地面放置的正方形框架ABCD,边长AB为30cm,在其正上方有一灯泡,在灯泡的照射下,正方形框架的横向影子A′B,D′C的长度和为6cm.那么灯泡离地面的高度为 .
(2)不改变图1中灯泡的高度,将两个边长为30cm的正方形框架按图2摆放,请计算此时横向影子A′B,D′C的长度和为多少?
(3)有n个边长为a的正方形按图3摆放,测得横向影子A′B,D′C的长度和为b,求灯泡离地面的距离.(写出解题过程,结果用含a,b,n的代数式表示)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列四种图形都是轴对称图形,其中对称轴条数最多的图形是
A. 等边三角形 B. 矩形 C. 菱形 D. 正方形
相关试题

