【题目】已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的![]() 还多1岁.
还多1岁.
(1)请用含m的式子表示这三人的年龄和;
(2)若这三人的年龄和为35岁,请你求出这三人的年龄.
参考答案:
【答案】(1)4m﹣5;(2)小明的年龄是10岁,小红的年龄是16岁,小华的年龄是9岁.
【解析】试题分析:(1)根据题意分别列出小明、小红和小华的年龄,再相加,去括号,合并同类项,即可求出这三名同学的年龄的和;
(2)根据题意可得关于m的方程,解方程求出m的值,再分别求出各自的年龄即可.
试题解析:(1)∵小明的年龄是m岁,
∴小红的年龄为(2m﹣4)岁,小华的年龄为[![]() (2m﹣4)+1]岁,
(2m﹣4)+1]岁,
∴三人的年龄和为:m+(2m﹣4)+![]() (2m﹣4)+1=m+2m﹣4+m﹣2+1=4m﹣5;
(2m﹣4)+1=m+2m﹣4+m﹣2+1=4m﹣5;
(2)根据题意得:4m﹣5=35,
解得:m=10,
∴2m﹣4=16,![]() (2m﹣4)+1=9,
(2m﹣4)+1=9,
答:小明的年龄是10岁,小红的年龄是16岁,小华的年龄是9岁.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2+px-3=0的一个根为-3,则它的另一根为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】元旦期间,商场中原价为 100元的某种商品经过两次连续降价后以每件81元出售,设这种商品每次降价的百分率相同,求这个百分率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠MAN=120°,AC平分∠MAN.B,D分别在射线AN,AM上.
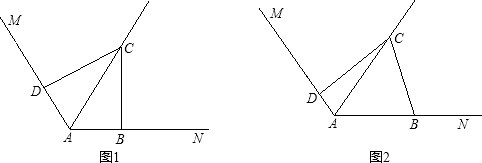
(1)在图(1)中,当∠ABC=∠ADC=90°时,求证:AD+AB=AC.
(2)若把(1)中的条件“∠ABC=∠ADC=90°”改为∠ABC+∠ADC=180°,其他条件不变,如图(2)所示.则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由. -
科目: 来源: 题型:
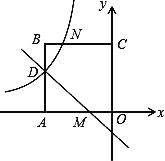
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y =
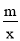 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于三角形的内心说法正确的是( )
A.内心是三角形三条角平分线的交点
B.内心是三角形三边中垂线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外
-
科目: 来源: 题型:
查看答案和解析>>【题目】解答
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.
证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.
(3)拓展与应用:如图(3),D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状.
相关试题

