【题目】解答
(1)如图(1),已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D,E.
证明:DE=BD+CE.
(2)如图(2),将(1)中的条件改为:在△ABC中,AB=AC,D,A,E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意锐角或钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由. 
(3)拓展与应用:如图(3),D,E是D,A,E三点所在直线m上的两动点(D,A,E三点互不重合),点F为∠BAC平分线上的一点,且△ABF和△ACF均为等边三角形,连接BD,CE,若∠BDA=∠AEC=∠BAC,试判断△DEF的形状. 
参考答案:
【答案】
(1)证明:∵BD⊥直线m,CE⊥直线m,
∴∠BDA=∠CEA=90°,
∵∠BAC=90°,
∴∠BAD+∠CAE=90°,
∵∠BAD+∠ABD=90°,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
(2)证明:成立.
∵∠BDA=∠BAC=α,
∴∠DBA+∠BAD=∠BAD+∠CAE=180°﹣α,
∴∠CAE=∠ABD,
∵在△ADB和△CEA中
 ,
,
∴△ADB≌△CEA(AAS),
∴AE=BD,AD=CE,
∴DE=AE+AD=BD+CE
(3)证明:△DEF是等边三角形.
由(2)知,△ADB≌△CEA,
BD=AE,∠DBA=∠CAE,
∵△ABF和△ACF均为等边三角形,
∴∠ABF=∠CAF=60°,
∴∠DBA+∠ABF=∠CAE+∠CAF,
∴∠DBF=∠FAE,
∵BF=AF
在△DBF和△EAF中
 ,
,
∴△DBF≌△EAF(SAS),
∴DF=EF,∠BFD=∠AFE,
∴∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,
∴△DEF为等边三角形
【解析】(1)根据BD⊥直线m,CE⊥直线m得∠BDA=∠CEA=90°,而∠BAC=90°,根据等角的余角相等得∠CAE=∠ABD,然后根据“AAS”可判断△ADB≌△CEA,则AE=BD,AD=CE,于是DE=AE+AD=BD+CE;(2)与(1)的证明方法一样;(3)由前面的结论得到△ADB≌△CEA,则BD=AE,∠DBA=∠CAE,根据等边三角形的性质得∠ABF=∠CAF=60°,则∠DBA+∠ABF=∠CAE+∠CAF,则∠DBF=∠FAE,利用“SAS”可判断△DBF≌△EAF,所以DF=EF,∠BFD=∠AFE,于是∠DFE=∠DFA+∠AFE=∠DFA+∠BFD=60°,根据等边三角形的判定方法可得到△DEF为等边三角形.
【考点精析】利用等边三角形的判定对题目进行判断即可得到答案,需要熟知三个角都相等的三角形是等边三角形;有一个角等于60°的等腰三角形是等边三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知小明的年龄是m岁,小红的年龄比小明的年龄的2倍少4岁,小华的年龄比小红的年龄的
 还多1岁.
还多1岁.(1)请用含m的式子表示这三人的年龄和;
(2)若这三人的年龄和为35岁,请你求出这三人的年龄.
-
科目: 来源: 题型:
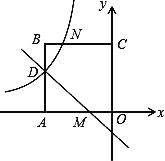
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形OABC的顶点O与坐标原点重合,点C的坐标为(0,3),点A在x轴的负半轴上,点D、M分别在边AB、OA上,且AD=2DB,AM=2MO,一次函数y=kx+b的图象过点D和M,反比例函数y =
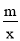 的图象经过点D,与BC的交点为N.
的图象经过点D,与BC的交点为N.(1)求反比例函数和一次函数的表达式;
(2)若点P在直线DM上,且使△OPM的面积与四边形OMNC的面积相等,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列关于三角形的内心说法正确的是( )
A.内心是三角形三条角平分线的交点
B.内心是三角形三边中垂线的交点
C.内心到三角形三个顶点的距离相等
D.钝角三角形的内心在三角形外
-
科目: 来源: 题型:
查看答案和解析>>【题目】枣庄乐园设置了一个秋千场所,如图所,秋千拉绳OB的长为3m,静止时,踏板到地面距离BD的长为0.6m(踏板厚度忽略不计).为安全起见,乐园管理处规定:儿童的“安全高度”为hm,成人的“安全高度”为2m(计算结果精确到0.1m)
(1)当摆绳OA与OB成45°夹角时,恰为儿童的安全高度,求h的长;
(2)某成人在玩秋千时,摆绳OC与OB的最大夹角为55°,问此人是否安全?(参考数据:
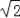 ≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)
≈1.41,sin55°≈0.82,cos55°≈0.57,tan55°≈1.43)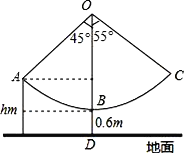
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=
 x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
x+4与x轴、y轴分别交于点A和点B,点C,D分别为线段AB,OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为.
A. (-3,0) B. (-6,0) C. (-
 ,0) D. (-
,0) D. (- ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】将抛物线y=x2﹣4x+1向左平移2个单位,再向上平移3个单位所得抛物线解析式为 .
相关试题

