【题目】如图所示,有一长方形的空地,长为![]() 米,宽为
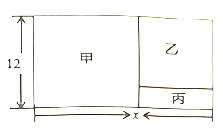
米,宽为![]() 米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.
米,建筑商把它分成甲、乙、丙三部分,甲和乙为正方形.现计划甲建筑成住宅区,乙建成商场丙开辟成公园.
![]() 请用含
请用含![]() 的代数式表示正方形乙的边长; ;
的代数式表示正方形乙的边长; ;
![]() 若丙地的面积为
若丙地的面积为![]() 平方米,请求出
平方米,请求出![]() 的值.
的值.
参考答案:
【答案】(1)(x12)米;(2)![]() 的值为20或16.
的值为20或16.
【解析】
(1)由甲和乙为正方形,且该地长为x米,宽为12米,可得出丙的长,也是乙的边长;
(2)由(1)求得丙的长,再求出丙的宽,即可得出丙的面积,由此列出方程,求解即可.
解:(1)因为甲和乙为正方形,结合图形可得丙的长为:(x12)米.
同样乙的边长也为(x12)米,
故答案为:(x12)米;
(2)结合(1)得,丙的长为:(x12)米,丙的宽为12(x12)=(24x)米,所以丙的面积为:(x12)(24x),
列方程得,(x12)(24x)=32
解方程得x1=20,x2=16.
答:![]() 的值为20或16.
的值为20或16.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(2017广东省深圳市)如图,抛物线
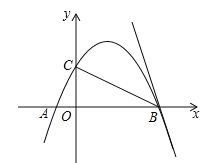
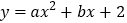 经过点A(﹣1,0),B(4,0),交y轴于点C;
经过点A(﹣1,0),B(4,0),交y轴于点C;(1)求抛物线的解析式(用一般式表示);
(2)点D为y轴右侧抛物线上一点,是否存在点D使
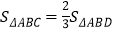 ?若存在请直接给出点D坐标;若不存在,请说明理由;
?若存在请直接给出点D坐标;若不存在,请说明理由;(3)将直线BC绕点B顺时针旋转45°,与抛物线交于另一点E,求BE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=8,AC=6.点D在边AB上,AD=4.5.△ABC的角平分线AE交CD于点F.
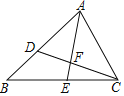
(1)求证:△ACD∽△ABC;
(2)求
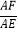 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将矩形ABCD沿GH对折,点C落在Q处,点D落在AB边上E处,EQ与BC相交于F,若AD=8 cm,AB=6 cm,AE=4cm,则△EBF的周长是______________ cm.
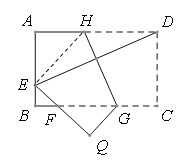
-
科目: 来源: 题型:
查看答案和解析>>【题目】我市某企业安排名
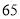 工人生产甲、乙两种产品,每人每天生产
工人生产甲、乙两种产品,每人每天生产 件甲产品或
件甲产品或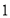 件乙产品,根据市场需求和生产经验,甲产品每件可获利
件乙产品,根据市场需求和生产经验,甲产品每件可获利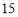 元,乙产品每件可获利
元,乙产品每件可获利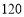 元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产
元,而实际生产中,生产乙产品需要额外支出一定的费用,经过核算,每生产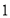 件乙产品,当天平均每件获利减少
件乙产品,当天平均每件获利减少 元,设每天安排
元,设每天安排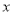 人生产乙产品.
人生产乙产品. 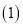 根据信息填表:
根据信息填表:产品种类
每天工人数(人)
每天产量(件)
每件产品可获利润(元)
甲
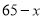
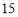
乙
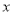
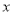
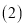 若每天生产甲产品可获得的利润比生产乙产品可获得的利润多
若每天生产甲产品可获得的利润比生产乙产品可获得的利润多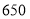 元,试问:该企业每天生产甲、乙产品可获得总利润是多少元?
元,试问:该企业每天生产甲、乙产品可获得总利润是多少元? -
科目: 来源: 题型:
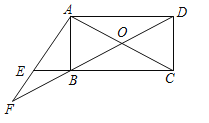
查看答案和解析>>【题目】如图,平行四边形ABCD的对角线AC、BD交于点O,点E在边CB的延长线上,且∠EAC=90°,AE2=EBEC.
(1)求证:四边形ABCD是矩形;
(2)延长DB、AE交于点F,若AF=AC,求证:AE=BF.
相关试题

