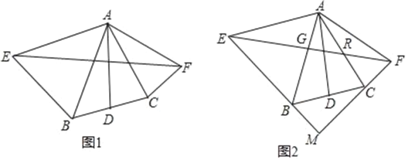
【题目】已知,如图AD为△ABC的中线,分别以AB和AC为一边在△ABC的外部作等腰三角形ABE和等腰三角形ACF,且AE=AB,AF=AC,连接EF,∠EAF+∠BAC=180°
(1)如图1,若∠ABE=63°,∠BAC=45°,求∠FAC的度数;
(2)如图1请探究线段EF和线段AD有何数量关系?并证明你的结论;
(3)如图2,设EF交AB于点G,交AC于点R,延长FC,EB交于点M,若点G为线段EF的中点,且∠BAE=70°,请探究∠ACB和∠CAF的数量关系,并证明你的结论.
参考答案:
【答案】(1)36°;(2)EF=2AD,见解析;(3)![]() ,见解析.
,见解析.
【解析】
(1)由等腰三角形的性质得出∠AEB=∠ABE=63°,由三角形内角和定理得出∠EAB=54°,推出∠EAB+2∠BAC+∠FAC=180°,即可得出结果;
(2)延长AD至H,使DH=AD,连接BH,由中线的性质得出BD=CD,由SAS证得△BDH≌△CDA得出HB=AC=AF,∠BHD=∠CAD,得出AC∥BH,由平行线的性质得出∠ABH+∠BAC=180°,证得∠EAF=∠ABH,由SAS证得△ABH≌△EAF,即可得出结论;
(3)由(2)得,AD=![]() EF,又点G为EF中点,得出EG=AD,由(2)△ABH≌△EAF得出∠AEG=∠BAD,由SAS证得△EAG≌△ABD得出∠EAG=∠ABC=70°,由已知得出∠EAB+2∠BAC+∠CAF=180°,推出∠BAC=55°-
EF,又点G为EF中点,得出EG=AD,由(2)△ABH≌△EAF得出∠AEG=∠BAD,由SAS证得△EAG≌△ABD得出∠EAG=∠ABC=70°,由已知得出∠EAB+2∠BAC+∠CAF=180°,推出∠BAC=55°-![]() ∠CAF,由三角形内角和定理得出∠BAC=180°-∠ABC-∠ACB=110°-∠ACB,即可得出结果.
∠CAF,由三角形内角和定理得出∠BAC=180°-∠ABC-∠ACB=110°-∠ACB,即可得出结果.
(1)∵AE=AB,
∴∠AEB=∠ABE=63°,
∴∠EAB=54°,
∵∠BAC=45°,∠EAF+∠BAC=180°,
∴∠EAB+2∠BAC+∠FAC=180°,
∴54°+2×45°+∠FAC=180°,
∴∠FAC=36°;
(2)EF=2AD;理由如下:
延长AD至H,使DH=AD,连接BH,如图1所示:
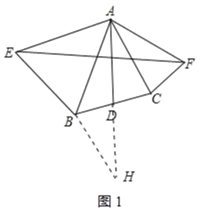
∵AD为△ABC的中线,
∴BD=CD,
在△BDH和△CDA中,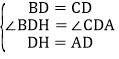 ,
,
∴△BDH≌△CDA(SAS),
∴HB=AC=AF,∠BHD=∠CAD,
∴AC∥BH,
∴∠ABH+∠BAC=180°,
∵∠EAF+∠BAC=180°,
∴∠EAF=∠ABH,
在△ABH和△EAF中,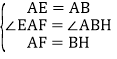 ,
,
∴△ABH≌△EAF(SAS),
∴EF=AH=2AD;
(3)![]() ;理由如下:
;理由如下:
由(2)得,AD=![]() EF,又点G为EF中点,
EF,又点G为EF中点,
∴EG=AD,
由(2)△ABH≌△EAF,
∴∠AEG=∠BAD,
在△EAG和△ABD中,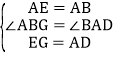 ,
,
∴△EAG≌△ABD(SAS),
∴∠EAG=∠ABC=70°,
∵∠EAF+∠BAC=180°,
∴∠EAB+2∠BAC+∠CAF=180°,
即:70°+2∠BAC+∠CAF=180°,
∴∠BAC+![]() ∠CAF=55°,
∠CAF=55°,
∴∠BAC=55°﹣![]() ∠CAF,
∠CAF,
∵∠ABC+∠ACB+∠BAC=180°,
∴∠BAC=180°﹣∠ABC﹣∠ACB=180°﹣70°﹣∠ACB=110°﹣∠ACB,
∴55°﹣![]() ∠CAF=110°﹣∠ACB,
∠CAF=110°﹣∠ACB,
∴∠ACB﹣![]() ∠CAF=55°.
∠CAF=55°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,A、B两地相距50千米,甲于某日下午1时骑自行车从A地出发驶往B地,乙也于同日下午骑摩托车按相同路线从A地出发驶往B地,如图所示,图中的折线PQR和线段MN分别表示甲、乙所行驶的路程S和时间t的关系.象回答下列问题:
(1)甲和乙哪一个出发的更早?早出发多长时间?
(2)甲和乙哪一个早到达B城?早多长时间?
(3)乙骑摩托车的速度和甲骑自行车在全程的平均速度分别是多少?
(4)请你根据图象上的数据,求出乙出发后多长时间追上甲?

-
科目: 来源: 题型:
查看答案和解析>>【题目】“五一”期间,某商场搞优惠促销,决定由顾客抽奖确定折扣.某顾客购买甲、乙两种商品,分别抽到七折(按售价的70%销售)和九折(按售价的90%销售),共付款386元,这两种商品原销售价之和为500元.问:这两种商品的原销售价分别为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了庆祝即将到来的2017年元旦,某校举行了书法比赛,赛后整理参赛同学的成绩,并制作成图表如下:
分数段
频数
频率
60≤x<70
30
0.15
70≤x<80
m
0.45
80≤x<90
60
n
90≤x≤100
20
0.1
请根据以上图表提供的信息,解答下列问题:
(1)这次共调查了 名学生;表中的数m= ,n= ;
(2)请在图中补全频数分布直方图;
(3)若绘制扇形统计图,分数段60≤x<70所对应扇形的圆心角的度数是 ;
(4)如果比赛成绩在80分以上(含80分)可获得奖励,那么获奖概率是多少?

-
科目: 来源: 题型:
查看答案和解析>>【题目】城市规划期间,欲拆除一电线杆AB,已知距电线杆AB水平距离14 m的D处有一大坝,背水坡CD的坡度i=1∶2,坝高CF为2 m,在坝顶C处测得杆顶A的仰角为30°,D、E之间是宽为2 m的人行道.
(1)求BF的长;
(2)在拆除电线杆AB时,为确保行人安全,是否需要将此人行道封上?请说明理由.(在地面上,以点B为圆心,以AB长为半径的圆形区域为危险区域,
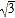 ≈1.732,
≈1.732,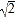 ≈1.414)
≈1.414)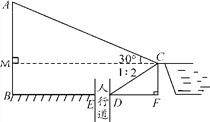
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知x=
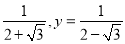 ;
;(1)求x2+y2﹣xy的值;
(2)若x的小数部分为a,y的小数部分为b,求(a+b)2+
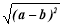 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某中学组织植树活动,按年级将七、八、九年级学生分成三个植树队,七年级植树x棵,八年级种的数比七年级种的数的2倍少26棵,九年级种的树比八年级种的树的一半多42棵.
(1)请用含x的式子表示三个队共种树多少棵.
(2)若这三个队共种树423棵,请你求出这三队各种了多少棵树.
相关试题

