【题目】如图①,在平面直角坐标系中,点A,B的坐标分别为(﹣1,0),(3,0),现同时将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,连接AC,BD,CD.
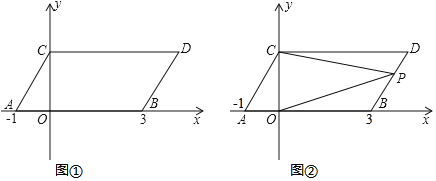
(1)求点C,D的坐标及S四边形ABDC;
(2)在y轴上是否存在一点Q,连接QA,QB,使S△QAB=S四边形ABDC若存在这样一点,求出点Q的坐标;若不存在,试说明理由;
(3)如图②,点P是线段BD上的一个动点,连接PC,PO,当点P在BD上移动时(不与B,D重合),求证:∠DCP+∠BOP=∠CPO.
参考答案:
【答案】(1)点C(0,2),点D(4,2),S四边形ABDC=8;(2)存在;Q点的坐标为(0,4)或(0,﹣4);(3)见解析.
【解析】
(1)根据平移的性质求出点C,D的坐标,再证明四边形ABDC是平行四边形,根据平行四边形的面积公式求解即可;
(2)设Q坐标为(0,m),列出方程求出m的值即可;
(3)作PE∥CD,根据平移的性质可得CD∥PE∥AB,再根据平行线的性质即可证明∠DCP+∠BOP=∠CPO.
(1)∵点A,B的坐标分别为(﹣1,0),(3,0),将点A,B分别向上平移2个单位长度,再向右平移1个单位长度,分别得到点A,B的对应点C,D,
∴点C(0,2),点D(4,2),AB=4,AB∥CD,AB=CD,
∴OC=2,四边形ABDC是平行四边形,
∴S四边形ABDC=4×2=8;
(2)设Q坐标为(0,m),
∴![]() ×4×|m|=8,
×4×|m|=8,
解得m=±4
∴Q点的坐标为(0,4)或(0,﹣4);
(3)如图,作PE∥CD,
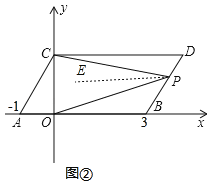
由平移可知:CD∥AB,
∴CD∥PE∥AB,
∴∠DCP=∠EPC,∠BOP=∠EPO,
∴∠DCP+∠BOP=∠EPC+∠EPO=∠CPO.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1在△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于点D,BE⊥MN于点E.
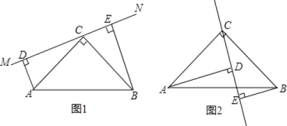
(1)求证:①△ADC≌△CEB;②DE=AD+BE.
(2)当直线MN绕点C旋转到图2的位置时,DE、AD、BE又怎样的关系?并加以证明.
-
科目: 来源: 题型:
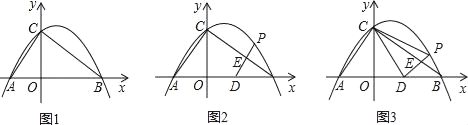
查看答案和解析>>【题目】已知:Rt△ABC的斜边长为5,斜边上的高为2,将这个直角三角形放置在平面直角坐标系中,使其斜边AB与x轴重合(其中OA<OB),直角顶点C落在y轴正半轴上(如图1).
(1)求线段OA、OB的长和经过点A、B、C的抛物线的关系式.
(2)如图2,点D的坐标为(2,0),点P(m,n)是该抛物线上的一个动点(其中m>0,n>0),连接DP交BC于点E.
①当△BDE是等腰三角形时,直接写出此时点E的坐标.
②又连接CD、CP(如图3),△CDP是否有最大面积?若有,求出△CDP的最大面积和此时点P的坐标;若没有,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△ABC中,BD平分∠ABC,CE平分∠ACB的邻补角∠ACM,若∠BDC=130°,∠E=50°,则∠BAC的度数是_______.
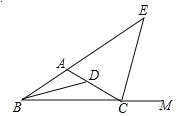
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在⊙O中,AB是⊙O的直径,AB=10,
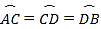 ,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED=
,点E是点D关于AB的对称点,M是AB上的一动点,下列结论:①∠BOE=60°;②∠CED= ∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )
∠DOB;③DM⊥CE;④CM+DM的最小值是10,上述结论中正确的个数是( )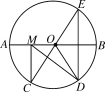
A. 1 B. 2 C. 3 D. 4
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,每个立方体的
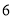 个面上分别写有
个面上分别写有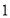 到
到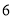 这
这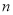 个自然数,并且任意两个相对面上所写两个数字之和为
个自然数,并且任意两个相对面上所写两个数字之和为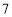 ,把这样的
,把这样的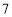 个立方体一个挨着一个地连接起来,紧挨着两个面上的数字之和为
个立方体一个挨着一个地连接起来,紧挨着两个面上的数字之和为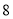 ,则图中“· ”所 在面上的数字是( )
,则图中“· ”所 在面上的数字是( )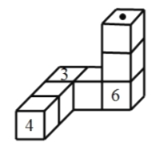
A.
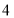 B.
B.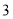
C.
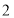 D.
D.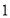
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=
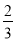 ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.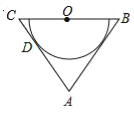
相关试题

