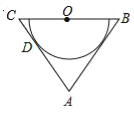
【题目】如图,在△ABC中,AB=AC,O为BC的中点,AC与半圆O相切于点D.
(1)求证:AB是半圆O所在圆的切线;
(2)若cos∠ABC=![]() ,AB=12,求半圆O所在圆的半径.
,AB=12,求半圆O所在圆的半径.
参考答案:
【答案】(1)详见解析;(2)![]() .
.
【解析】
试题分析:(1)根据等腰三角形的性质,可得OA,根据角平分线的性质,可得OE,根据切线的判定,可得答案;(2)根据锐角三角函数,可得OB的长,根据勾股定理,可得OA的长,根据三角形的面积,可得OE的长.
试题解析:(1)证明:如图1,

作OD⊥AC于D,OE⊥AB于E,
∵AB=AC,O为BC的中点,
∴∠CAO=∠BAO.
∵OD⊥AC于D,OE⊥AB于E,
∴OD=OE,
∵AB经过圆O半径的外端,
∴AB是半圆O所在圆的切线;
(2)cos∠ABC=![]() ,AB=12,得OB=8.
,AB=12,得OB=8.
由勾股定理,得AO=4![]() .
.
由三角形的面积,得S△AOB=![]() ABOE=
ABOE=![]() OBAO,
OBAO,
∴OE=![]() =
=![]() ,
,
即半圆O所在圆的半径是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对一个假命题举反例时,应使所举反例( )
A.满足命题的条件,并满足命题的结论
B.满足命题的条件,但不满足命题的结论
C.不满足命题的条件,但满足命题的结论
D.不满足命题的条件,也不满足命题的结论
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算中,正确的是( )
A.3x+2x2=5x2
B.﹣ab﹣ab=﹣2ab
C.2a2b﹣a2b=1
D.7x+5x=12x2 -
科目: 来源: 题型:
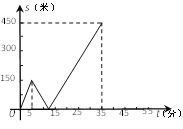
查看答案和解析>>【题目】甲乙两人匀速从同一地点到1500米处的图书馆看书,甲出发5分钟后,乙以50米/分的速度沿同一路线行走.设甲乙两人相距
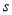 (米),甲行走的时间为
(米),甲行走的时间为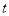 (分),
(分),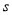 关于
关于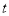 的函数函数图像的一部分如图所示.
的函数函数图像的一部分如图所示.(1)求甲行走的速度;
(2)在坐标系中,补画
 关于
关于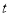 函数图象的其余部分;
函数图象的其余部分;(3)问甲、乙两人何时相距360米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】嘉淇同学要证明命“两相对边分别相等的四边形是平行四边形”是正确的,她先用尺规作出了如图的四边形ABCD,并写出了如下不完整的已知和求证.
已知:如图,在四边形ABCD中,
BC=AD,
AB=____.
求证:四边形ABCD是____四过形.
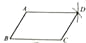
(1)在方框中填空,以补全已知和求证;
(2)按嘉淇的想法写出证明:
证明:

(3)用文宇叙述所证命题的逆命题为____________________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(本小题10分)
如图1,以□BMDC的两相邻边CB、CD为腰,在□BMDC的外侧,作两个等腰Rt△CBF和Rt△CDH,则□ BMDC中与C相对的顶点M与这两等腰直角三角形的两顶点F、H形成一个新的等腰直角三角形FMH. 请证明△FMH为等腰直角三角形。
如图2,以□BMDC的两相邻边CB、CD为腰, 在□BMDC的外侧,作两个等腰△CBF和△CDH,使其顶角∠CBF=∠CDH=α,则□BMDC中与C相对的顶点M与两等腰三角形的两顶点F、H形成一个新的等腰三角形,写出顶角∠FMH的度数。试说明理由。
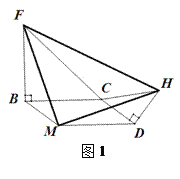
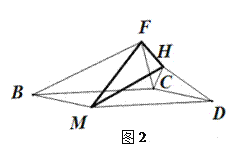
-
科目: 来源: 题型:
查看答案和解析>>【题目】a是一位数,b是两位数.把a放在b的右边,所得的三位数可以表示为( )
A. 100b+a B. 10b+a C. ba D. b+a
相关试题

