[题目]如图.在四边形ABCD中.AB∥CD.AD∥BC.AC.BD相交于O.则图中能够全等的三角形共有( )对．A.4B.3C.2D.1 题目和参考答案 ——青夏教育精英家教网—

科目： 来源： 题型：

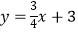【题目】如图，直线与x轴交于点A，与直线 y=kx-3交于点C（c,6），直线与y轴交于点B，连接AB．
（1）求k的值；
（2）求证：∠CAO=∠BAO；
（3）P为OA上一点，连结PB，M为PB中点，延长MO交直线AC于点N，若OP=x， ,求y关于x的函数表达式．
查看答案和解析>>
科目： 来源： 题型：

【题目】抛物线C：y=x2+bx+c 交轴于点A（0，-1）且过点， P是抛物线C上一个动点，过P作PB∥OA，以P为圆心，2为半径的圆交PB于C、D两点（点D位于点C下方）．

（1）求抛物线C的解析式；
（2）连接AP交⊙P于点E，连接DE，AC．若ΔACP是以CP为直角边的直角三角形，求∠EDC的度数；
（3）若当点P经过抛物线C上所有的点后，点D随之经过的路线被直线截得的线段长为8，求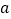的值．
查看答案和解析>>
科目： 来源： 题型：

【题目】我们知道：有一内角为直角的三角形叫做直角三角形．类似地，我们定义：有一内角为45°的三角形叫做半直角三角形．如图，在平面直角坐标系中，O为原点，A（4，0），B（－4，0），D是y轴上的一个动点，∠ADC=90°(A、D、C按顺时针方向排列)， BC与经过A，B，D三点的⊙M交于点E，DE平分∠ADC，连结AE，BD．显然△DCE，△DEF，△DAE是半直角三角形．

（1）求证：△ABC是半直角三角形；
（2）求证：∠DEC=∠DEA；
（3）若点D的坐标为（0，8），
①求AE的长；
②记BC与AD的交点为F，求ΔACF与ΔBCA的面积之比．
查看答案和解析>>
科目： 来源： 题型：

【题目】已知，如图，在ABCD中，BF平分∠ABC交AD于点F，AE⊥BF于点O，交BC于点E，连接EF．
（1）求证：四边形ABEF是菱形：
（2）若菱形ABEF的周长为16，∠BEF＝120°，求AE的大小．
查看答案和解析>>
科目： 来源： 题型：

【题目】某校为了解本校的选修课教学，校教务处在七、八年级所有班级中，每班随机抽取了6名学生，并对他们的选修课喜欢程度情况进行了问卷调查，喜欢程度分为：“A﹣非常喜欢”、“B﹣比较喜欢”、“C﹣不太喜欢”、“D﹣很不喜欢”，针对这个题目，问卷时要求每位被调查的学生必须从中选一项且只能选一项．现将统计结果绘制成如下两幅不完整的统计图．
请你根据以上提供的信息，解答下列问题：
（1）补全上面的条形统计图和扇形统计图；
（2）若接核七、八年级共有700名学生，请你估境该年级学生中对远修课“不太喜欢”的有多少人？
查看答案和解析>>
科目： 来源： 题型：

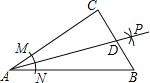
【题目】如图，在Rt△ABC中，∠C=90°，以A为圆心，以任意长为半径画弧，分别交AC、AB于点M、N，再分别以点M、N为圆心，以一个定长为半径画弧，两弧交于点P，作射线AP交BC于点D．若AC=8，BC=6，则CD的长为(　　)
A.B.C.D.
查看答案和解析>>