【题目】某火车站现有甲种货物1530吨,乙种货物1150吨,安排一列火车将货物运往某城市。火车可挂A、B两种不同规格的车厢50节,已知用一节A型车厢费用0.5 万元,用一节B型车厢的费用0.8万元.
(1)已知甲种货物35吨和乙种货物15吨可装满一节A型车厢,甲种货物25吨和乙种货物35吨可以装满一节B型车厢,请设计A、B两种车厢的节数,有几种运输方案?请一一写出.
(2)哪个方案运费最少?最少运费多少元?
参考答案:
【答案】(1)三种方案:①A车厢28节,B车厢22节;②A车厢29节,B车厢21节;③A车厢30节,B车厢20节;(2)方案③运费最少为31万元.
【解析】
(1)根据甲种货物的总重量≥1530,乙种货物的总重量≥1150,列方程组求解,注意自变量只能取整数.
(2)由一次函数的增减性解答.
(1)由题意得:y=0.5x+0.8(50x)=0.3x+40,故所求函数关系为y=0.3x+40;
根据题意可列不等式组
![]()
解得28![]() x
x![]() 30
30
所以,方案有以下几种
①A:28, B:22
②A:29, B:21
③A:30, B:20;
(2)由第一问不难看出x值越大,y值越小
因此方案③运费最少
y=0.3×30+40=31,
所以,在这些方案中,③方案的总运费最少,最少运费是31万元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)
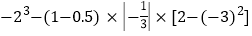 ;
; (2)
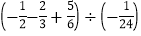 ;
; (3)先化简,再求值
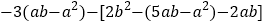 ,其中
,其中 与
与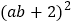 互为相反数.
互为相反数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC是等腰直角三角形,∠ACB=90°,分别以AB,AC为直角边向外作等腰直角△ABD和等腰直角△ACE,G为BD的中点,连接CG,BE,CD,BE与CD交于点F.
(1)判断四边形ACGD的形状,并说明理由.
(2)求证:BE=CD,BE⊥CD.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
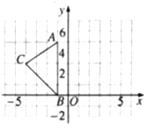
⑴请画出△ABC关于y轴对称的△A’B’C’(其中A’,B’,C’分別是A,B,C的对应点,不写画法);
⑵直接写出A’,B’,C’三点的坐标:A’ ( ),B’( ),C’( );
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的第一条边的长是
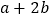 ,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。
,第二条边长是第一条边长的2倍少3,第三条边比第二条边短5。(1)用含
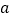 、
、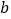 的式子表示这个三角形的周长;
的式子表示这个三角形的周长;(2)当
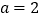 ,
,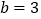 时,求这个三角形的周长;
时,求这个三角形的周长;(3)当
 ,三角形的周长为 39时,求各边长。
,三角形的周长为 39时,求各边长。 -
科目: 来源: 题型:
查看答案和解析>>【题目】△ABC和△ADE都是等腰直角三角形, ∠BAC=∠DAE=90°.
(1)如图1,点D、E在AB、AC上,则BD,CE满足怎样的数量关系和位置关系?(直接写出答案)
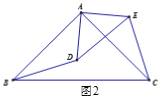
(2)如图2,点D在△ABC内部, 点E在△ABC外部,连结BD, CE, 则BD,CE满足怎样的数量关系和位置关系?请说明理由.
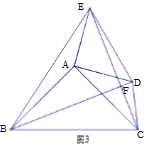
(3)如图3,点D,E都在△ABC外部,连结BD, CE, CD, EB,BD, 与CE相交于H点. 若BD=
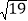 ,求四边形BCDE的面积.
,求四边形BCDE的面积.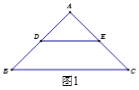
-
科目: 来源: 题型:
查看答案和解析>>【题目】有一快递小哥骑电动车需要在规定的时间把快递送到某地,若他以
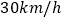 的速度行驶就会提前2分钟到达,如果他以
的速度行驶就会提前2分钟到达,如果他以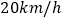 的速度行驶就要迟到6分钟。
的速度行驶就要迟到6分钟。(1)快递小哥行驶的路程是多少千米;
(2)当快递小哥以
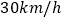 的速度行驶10分钟后,因某段路拥堵耽误了3分钟,为了刚好在规定时间到达,快递小哥应以怎祥的速度行驶。
的速度行驶10分钟后,因某段路拥堵耽误了3分钟,为了刚好在规定时间到达,快递小哥应以怎祥的速度行驶。
相关试题

