【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )
A.r≥1
B.1≤r≤ ![]()
C.1≤r≤ ![]()
D.1≤r≤4
参考答案:
【答案】C
【解析】解:作OD⊥AB于D,OE⊥BC于E,OF⊥AC于F,连接OA、OB,如图所示
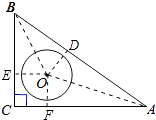
则四边形OECF是正方形,
∴OF=CF=OE=CE,
∵∠C=90°,AC=4,BC=3,
∴AB= ![]() =5,
=5,
∵O是△ABC的内心,
∴CE=CF=OF=OE= ![]() (AC+BC﹣AB)=1,
(AC+BC﹣AB)=1,
∴AF=AC﹣CF=3,BE=BC﹣CE=2,
∴OA= ![]() ,OB=
,OB= ![]() =
= ![]() ,
,
当r=1时,以O为圆心,r为半径的圆与线段AB有唯一交点;
当1<r≤ ![]() 时,以O为圆心,r为半径的圆与线段AB有两个交点;
时,以O为圆心,r为半径的圆与线段AB有两个交点;
当 ![]() <r≤
<r≤ ![]() 时,以O为圆心,r为半径的圆与线段AB有1个交点;
时,以O为圆心,r为半径的圆与线段AB有1个交点;
∴以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是1≤r≤ ![]() ;
;
所以答案是:C
【考点精析】掌握直线与圆的三种位置关系和三角形的内切圆与内心是解答本题的根本,需要知道直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点;三角形的内切圆的圆心是三角形的三条内角平分线的交点,它叫做三角形的内心.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)
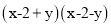
(3)

(4)
 (用公式计算)
(用公式计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:

(1)△AGM∽△BME;
(2)若M为AB中点,则 ;
;
(3)△AGM的周长为2a. -
科目: 来源: 题型:
查看答案和解析>>【题目】完成下列推理过程
已知:∠C+∠CBD=180°,∠ABD=85°,∠2=60°,求∠A的度数.

解:∵∠C+∠CBD=180°(已知)
∴DB∥CE( )
∴∠1= ( )
∵∠2=∠3( )
∴∠1=∠2=60° ( )
又∵ ∠ABD=85°(已知)
∴∠A=180°-∠ABD-∠1= (三角形三内角和为180°)
-
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6
 B. 6C. 3
B. 6C. 3 D. 3+3
D. 3+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的边长为3,点A、C分别在x轴,y轴的正半轴上,点D(1,0)在OA上,P是OB上一动点,则PA+PD的最小值为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB分别切⊙O于点A、B,若∠P=70°,则∠C的大小为(度).

相关试题

