【题目】完成下列推理过程
已知:∠C+∠CBD=180°,∠ABD=85°,∠2=60°,求∠A的度数.

解:∵∠C+∠CBD=180°(已知)
∴DB∥CE( )
∴∠1= ( )
∵∠2=∠3( )
∴∠1=∠2=60° ( )
又∵ ∠ABD=85°(已知)
∴∠A=180°-∠ABD-∠1= (三角形三内角和为180°)
参考答案:
【答案】同旁内角互补,两直线平行;∠3;两直线平行,同位角相等;对顶角相等;等量代换;35°.
【解析】
根据平行线的判定定理和性质定理、三角形内角和定理填空即可.
解:∵∠C+∠CBD=180°(已知)
∴DB∥CE(同旁内角互补,两直线平行)
∴∠1=∠3(两直线平行,同位角相等)
∵∠2=∠3(对顶角相等)
∴∠1=∠2=60°(等量代换)
又∵ ∠ABD=85°(已知)
∴∠A=180°-∠ABD-∠1=35°(三角形三内角和为180°)
故答案为:同旁内角互补,两直线平行;∠3;两直线平行,同位角相等;对顶角相等;等量代换;35°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】七年级进行法律知识竞赛,共有30道题,答对一道题得4分,不答或答错一道题扣2分.
(1)小红同学参加了竞赛,成绩是96分,请问小红在竞赛中答对了多少题?
(2)小明也参加了竞赛,考完后他说:“这次竟赛中我一定能拿到110分.”请问小明有没有可能拿到110分?试用方程的知识来说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:
(1)

(2)
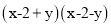
(3)

(4)
 (用公式计算)
(用公式计算) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,折叠边长为a的正方形ABCD,使点C落在边AB上的点M处(不与点A,B重合),点D落在点N处,折痕EF分别与边BC、AD交于点E、F,MN与边AD交于点G.证明:

(1)△AGM∽△BME;
(2)若M为AB中点,则 ;
;
(3)△AGM的周长为2a. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=4,BC=3,O是△ABC的内心,以O为圆心,r为半径的圆与线段AB有交点,则r的取值范围是( )

A.r≥1
B.1≤r≤
C.1≤r≤
D.1≤r≤4 -
科目: 来源: 题型:
查看答案和解析>>【题目】把边长为3的正方形ABCD绕点A顺时针旋转45°得到正方形AB′C′D′,边BC与D′C′交于点O,则四边形ABOD′的周长是( )

A. 6
 B. 6C. 3
B. 6C. 3 D. 3+3
D. 3+3
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形OABC的边长为3,点A、C分别在x轴,y轴的正半轴上,点D(1,0)在OA上,P是OB上一动点,则PA+PD的最小值为_____.

相关试题

