【题目】如图,AB=AC,FD⊥BC于D,DE⊥AB于E,若∠AFD=145°,则∠EDF=度.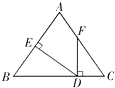
参考答案:
【答案】55
【解析】解:∵∠AFD=145°,∴∠CFD=35°
又∵FD⊥BC于D,DE⊥AB于E
∴∠C=180°﹣(∠CFD+∠FDC)=55°
∵AB=AC
∴∠B=∠C=55°,∴∠A=70°
根据四边形内角和为360°可得:
∠EDF=360°﹣(∠AED+∠AFD+∠A)=55°
∴∠EDF为55°.
故填55.
【考点精析】通过灵活运用垂线的性质和三角形的内角和外角,掌握垂线的性质:1、过一点有且只有一条直线与己知直线垂直.2、垂线段最短;三角形的三个内角中,只可能有一个内角是直角或钝角;直角三角形的两个锐角互余;三角形的一个外角等于和它不相邻的两个内角的和;三角形的一个外角大于任何一个和它不相邻的内角即可以解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】以x为自变量的二次函数y=x2﹣2(b﹣2)x+b2﹣1的图象不经过第三象限,则实数b的取值范围是( )
A.b≥
B.b≥1或b≤﹣1
C.b≥2
D.1≤b≤2 -
科目: 来源: 题型:
查看答案和解析>>【题目】下图是交警在一个路口统计的某个时段来往车辆的车速(单位:千米/小时)情况,则下列关于车速描述错误的是( )
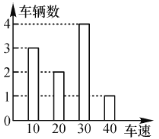
A. 平均数是23 B. 中位数是25 C. 众数是30 D. 方差是129
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m, CE⊥直线m,垂足分别为点D、E.证明:DE=BD+CE.
(2)如图②,将(1)中的条件改为:在△ABC中,AB=AC,D、A、E三点都在直线m上,并且有∠BDA=∠AEC=∠BAC=α,其中α为任意钝角.请问结论DE=BD+CE是否成立?如成立,请你给出证明;若不成立,请说明理由.

-
科目: 来源: 题型:
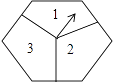
查看答案和解析>>【题目】如图是一个能自由转动的正六边形转盘,这个转盘被三条分割线分成形状相同,面积相等的三部分,且分别标有“1”、“2”、“3”三个数字,指针的位置固定不动,让转盘自由转动两次,当每次转盘停止后,记录指针指向的数(当指针指向分割线时,视其指向分割线左边的区域),则两次指针指向的数都是奇数的概率为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的不等式组
 的解集为﹣1<x<1,则(a+b)2017的值是( )
的解集为﹣1<x<1,则(a+b)2017的值是( )
A.1
B.
C.﹣1
D.﹣
-
科目: 来源: 题型:
查看答案和解析>>【题目】在Rt△ABC中,∠ACB=90°,D,E是边AB上两点,且CE所在直线垂直平分线段AD,CD平分∠BCE,AC=5cm,则BD的长为( )
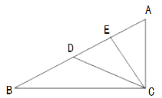
A. 5cm B. 6cm C. 7cm D. 8cm
相关试题

