【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于A(﹣2,m),B
的图象交于A(﹣2,m),B
(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
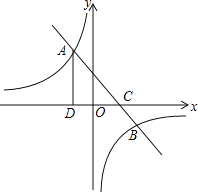
(1)求这两个函数的解析式:
(2)求△ADC的面积.
参考答案:
【答案】(1)![]() ;y=﹣x+2;(2)S△ADC=8
;y=﹣x+2;(2)S△ADC=8
【解析】
(1)因为反比例函数过A、B两点,所以可求其解析式和m的值,从而知A点坐标,进而求一次函数解析式.
(2)先求出直线AB与与x轴的交点C的坐标,再根据三角形的面积公式求解即可.
解:(1)∵反比例函数![]() 的图象过B(4,﹣2)点,∴k=4×(﹣2)=﹣8.
的图象过B(4,﹣2)点,∴k=4×(﹣2)=﹣8.
∴反比例函数的解析式为![]() .
.
∵反比例函数![]() 的图象过点A(﹣2,m),∴
的图象过点A(﹣2,m),∴![]() .∴A(﹣2,4).
.∴A(﹣2,4).
∵一次函数y=ax+b的图象过A(﹣2,4),B(4,﹣2)两点,
∴![]() ,解得
,解得![]() .
.
∴一次函数的解析式为y=﹣x+2;
(2)∵直线AB:y=﹣x+2交x轴于点C,∴C(2,0).
∵AD⊥x轴于D,A(﹣2,4),∴CD=2﹣(﹣2)=4,AD=4.
∴S△ADC=![]() CDAD=
CDAD=![]() ×4×4=8.
×4×4=8.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数 y1=k1x与
 的图象都经过点(2,2).
的图象都经过点(2,2).(1)填空:k1= ,k2= ;
(2)在同一坐标系中作出这两个函数的图象;
(3)直接写出当y1>y2时,自变量x的取值范围: .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,下列结论:①b<0;②4a+2b+c<0;③a﹣b+c>0;④(a+c)2<b2 . 其中正确的结论是( )

A.①②
B.①③
C.①③④
D.①②③④ -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(﹣2,y1),B(﹣1,y2)和C(3,y3)都在反比例函数y=
 的图象上,则y1 , y2 , y3的大小关系为 . (用“<”连接)
的图象上,则y1 , y2 , y3的大小关系为 . (用“<”连接) -
科目: 来源: 题型:
查看答案和解析>>【题目】声音在空气中传播的速度
 (简称音速)与气温
(简称音速)与气温 的关系如下表:
的关系如下表:气温

0
5
10
15
20
音速

331
334
337
340
343
(1)这一变化过程中,自变量和因变量各是什么?
(2)音速
 与气温
与气温 之间的关系式.
之间的关系式.(3)气温

 时,某人看到烟花燃放
时,某人看到烟花燃放 后才听到声音,那么此人与燃放烟花的所在地约相距多远?
后才听到声音,那么此人与燃放烟花的所在地约相距多远? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1是一个长为
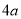 、宽为
、宽为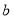 的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)
的长方形,沿图中虚线用剪刀平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图2)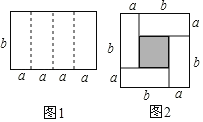
(1)观察图2请你写出
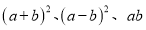 之间的等量关系是________;
之间的等量关系是________;(2)根据(1)中的结论,若
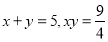 ,则
,则 ________;
________;(3)拓展应用:若
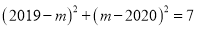 ,求
,求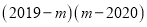 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】我县万德隆商场有A、B两种商品的进价和售价如表:
商品
价格
A
B
进价(元/件)
m
m+20
售价(元/件)
160
240
已知:用2400元购进A种商品的数量与用3000元购进B种商品的数量相同.
(1)求m的值;
(2)该商场计划同时购进的A、B两种商品共200件,其中购进A种商品x件,实际进货时,生产厂家对A种商品的出厂价下调a(50<a<70)元出售,若商场保持同种商品的售价不变,商场售完这200件商品的总利润为y元.
①求y关于x的函数关系式;
②若限定A种商品最多购进120件最少购进100件,请你根据以上信息,设计出使该商场获得最大利润的进货方案.
相关试题

