【题目】 如图①点C在线段AB上,点M、N分别是AC、BC的中点,且满足AC=a,BC=b.
(1)若a=4 cm,b=6 cm,求线段MN的长;
(2)若点C为线段AB上任意一点,其它条件不变,你能猜想MN的长度吗?直接写出你的猜想结果;
(3)若点C在线段AB的延长线上,其它条件不变,你能猜想MN的长度吗?请在图②中画出图形,写出你的猜想并说明理由.
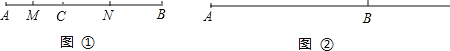
参考答案:
【答案】(1)5cm;(2)![]() ;(3)画图见解析,MN=
;(3)画图见解析,MN=![]() (a﹣b),理由见解析.
(a﹣b),理由见解析.
【解析】
(1)根据AC和BC分别求出MC和NC的长度,相加,即可得出答案;
(2)步骤同(1);
(3)根据AC和BC分别求出MC和NC的长度,相减,即可得出答案.
解:(1)∵M、N分别是AC、BC的中点,
∴MC=![]() AC,CN=
AC,CN=![]() BC,
BC,
∴MN=MC+CN
=![]() AC+
AC+![]() BC
BC
=![]() ×4+
×4+![]() ×6
×6
=5cm,
所以MN的长为5cm.
(2)同(1),MN=![]() AC+
AC+![]() CB=
CB=![]() (AC+CB)=
(AC+CB)=![]() (a+b).
(a+b).
(3)图如右,MN=![]() (a﹣b).
(a﹣b).

理由:由图知MN=MC﹣NC
=![]() AC﹣
AC﹣![]() BC
BC
=![]() a﹣
a﹣![]() b
b
=![]() (a﹣b).
(a﹣b).
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面一段文字:
问题:0.
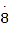 能用分数表示吗?
能用分数表示吗?探求:步骤①设x=0.
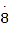 ,
,步骤②10x=10×0.
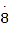 ,
,步骤③10x=8.
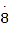 ,
,步骤④10x=8+0.
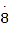 ,
,步骤⑤10x=8+x,
步骤⑥9x=8,
步骤⑦x=
 .
.根据你对这段文字的理解,回答下列问题:
(1)步骤①到步骤②的依据是______;
(2)仿照上述探求过程,请你尝试把0.
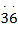 表示成分数的形式.
表示成分数的形式. -
科目: 来源: 题型:
查看答案和解析>>【题目】定义:若A﹣B=1,则称A与B是关于1的单位数.
(1)3与______是关于1的单位数,x﹣3与______是关于1的单位数.(填一个含x的式子)
(2)若A=3x(x+2)﹣1,
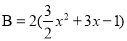 ,判断A与B是否是关于1的单位数,并说明理由.
,判断A与B是否是关于1的单位数,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】 请阅读下列材料,并解答相应的问题:
将若干个数组成一个正方形数阵,若任意一行,一列及对角线上的数字之和都相等,则称具有这种性质的数字方阵为“幻方”中国古代称“幻方”为“河图“、“洛书“等,例如,下面是三个三阶幻方,是将数字1,2,3,4,5,6,7,8,9填入到3×3的方格中得到的,其每行、每列、每条对角线上的三个数之和相等.
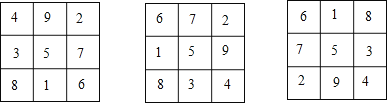
(1)设图1的三阶幻方中间的数字是x,用x的代数式表示幻方中9个数的和为 ;
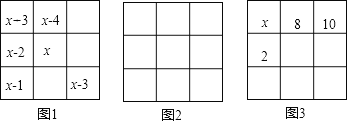
(2)请你将下列九个数:﹣10、﹣8、﹣6、﹣4、﹣2、0、2、4、6分别填入图2方格中,使得每行、每列、每条对角线上的三个数之和都相等;
(3)图3是一个三阶幻方,那么标有x的方格中所填的数是 ;
(4)如图4所示的每一个圆中分别填写了1、2、3…19中的一个数字(不同的圆中填写的数字各不相同),使得图中每一个横或斜方向的线段上几个圆内的数之和都相等,现在已知该图中七个圆内的数字,则图中的x= ,y= .

-
科目: 来源: 题型:
查看答案和解析>>【题目】 观察下列两个等式:2+2=2×2,3+
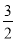 =3×
=3×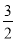 ,给出定义如下:我们称使等式a+b=ab成立的一对有理数a,b为“有趣数对”,记为(a,b)如:数对(2,2),(3,
,给出定义如下:我们称使等式a+b=ab成立的一对有理数a,b为“有趣数对”,记为(a,b)如:数对(2,2),(3,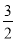 )都是“有趣数对”.
)都是“有趣数对”.(1)数对(0,0),(5,
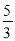 )中是“有趣数对”的是 ;
)中是“有趣数对”的是 ;(2)若(a,
 )是“有趣数对”,求a的值;
)是“有趣数对”,求a的值;(3)请再写出一对符合条件的“有趣数对” ;
(注意:不能与题目中已有的“有趣数对”重复)
(4)若(a2+a,4)是“有趣数对”求3﹣2a2﹣2a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,有下列说法:①甲、乙同学都骑行了18km;②甲、乙同学同时到达B地;③甲停留前、后的骑行速度相同;④乙的骑行速度是
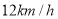 ;其中正确的说法是( )
;其中正确的说法是( )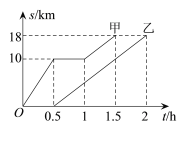
A. ①③B. ①④C. ②④D. ②③
-
科目: 来源: 题型:
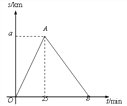
查看答案和解析>>【题目】某市举行长跑比赛,运动员从甲地出发跑到乙地后,又沿原路线跑回起点甲地.如图是某运 动员离开甲地的路程 s(km)与跑步时间 t(min)之间的函数关系(OA、OB 均为线段).已 知该运动员从甲地跑到乙地时的平均速度是 0.2 km/min,根据图像提供的信息,解答下列问 题:
(1)a= km;
(2)组委会在距离起点甲地 3 km 处设立了一个拍摄点 P,该运动员从第一次过 P 点到第二
次过 P 点所用的时间为 24 min.
①求 AB 所在直线的函数表达式;
②该运动员跑完全程用时多少 min?
相关试题

