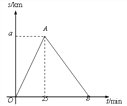
【题目】某市举行长跑比赛,运动员从甲地出发跑到乙地后,又沿原路线跑回起点甲地.如图是某运 动员离开甲地的路程 s(km)与跑步时间 t(min)之间的函数关系(OA、OB 均为线段).已 知该运动员从甲地跑到乙地时的平均速度是 0.2 km/min,根据图像提供的信息,解答下列问 题:
(1)a= km;
(2)组委会在距离起点甲地 3 km 处设立了一个拍摄点 P,该运动员从第一次过 P 点到第二
次过 P 点所用的时间为 24 min.
①求 AB 所在直线的函数表达式;
②该运动员跑完全程用时多少 min?
参考答案:
【答案】(1)5;(2) s=![]() ;(3) 60 min.
;(3) 60 min.
【解析】试题分析:(1)根据路程=速度×时间,即可求出a值;
(2)①根据点O、A的坐标,利用待定系数法即可求出线段OA的函数表达式,根据一次函数图象上点的坐标特征可求出第一次经过点P的时间,进而可得出第二次经过点P的时间,再根据点A的坐标及(39,3),利用待定系数法即可求出AB所在直线的函数表达式;
②根据一次函数图象上点的坐标特征,求出AB所在直线的函数表达式中当s=0时t的值,此题得解.
试题解析:解:(1)∵从甲地跑到乙地时的平均速度是0.2 km/min用时25分钟,∴a=0.2×25=5(千米).故答案为:5.
(2)①设线段OA的函数表达式为s=mt+n,将O(0,0)、A(25,5)代入s=mt+n中,得: ![]() ,解得:
,解得: 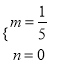 ,∴线段OA的函数表达式为s=
,∴线段OA的函数表达式为s=![]() t(0≤t≤25),∴当s=
t(0≤t≤25),∴当s=![]() t=3时,t=15.∵该运动员从第一次过P点到第二次过P点所用的时间为24min,∴该运动员从起点到第二次经过P点所用的时间是15+24=39(min),∴直线AB经过点(25,5),(39,3).设AB所在直线的函数表达式为s=kt+b,将(25,5)、(39,3)代入s=kt+b中,得:
t=3时,t=15.∵该运动员从第一次过P点到第二次过P点所用的时间为24min,∴该运动员从起点到第二次经过P点所用的时间是15+24=39(min),∴直线AB经过点(25,5),(39,3).设AB所在直线的函数表达式为s=kt+b,将(25,5)、(39,3)代入s=kt+b中,得: ![]() ,解得:
,解得: 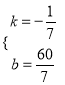 ,∴AB所在直线的函数表达式为s=﹣
,∴AB所在直线的函数表达式为s=﹣![]() t+
t+![]() .
.
②该运动员跑完赛程用的时间即为直线AB与x轴交点的横坐标,∴当s=0时,﹣![]() t+
t+![]() =0,解得:t=60,∴该运动员跑完赛程用时60分钟.
=0,解得:t=60,∴该运动员跑完赛程用时60分钟.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 如图①点C在线段AB上,点M、N分别是AC、BC的中点,且满足AC=a,BC=b.
(1)若a=4 cm,b=6 cm,求线段MN的长;
(2)若点C为线段AB上任意一点,其它条件不变,你能猜想MN的长度吗?直接写出你的猜想结果;
(3)若点C在线段AB的延长线上,其它条件不变,你能猜想MN的长度吗?请在图②中画出图形,写出你的猜想并说明理由.
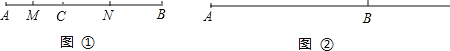
-
科目: 来源: 题型:
查看答案和解析>>【题目】 观察下列两个等式:2+2=2×2,3+
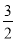 =3×
=3×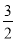 ,给出定义如下:我们称使等式a+b=ab成立的一对有理数a,b为“有趣数对”,记为(a,b)如:数对(2,2),(3,
,给出定义如下:我们称使等式a+b=ab成立的一对有理数a,b为“有趣数对”,记为(a,b)如:数对(2,2),(3,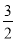 )都是“有趣数对”.
)都是“有趣数对”.(1)数对(0,0),(5,
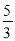 )中是“有趣数对”的是 ;
)中是“有趣数对”的是 ;(2)若(a,
 )是“有趣数对”,求a的值;
)是“有趣数对”,求a的值;(3)请再写出一对符合条件的“有趣数对” ;
(注意:不能与题目中已有的“有趣数对”重复)
(4)若(a2+a,4)是“有趣数对”求3﹣2a2﹣2a的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名同学骑自行车从A地出发沿同一条路前往B地,他们离A地的距离s(km)与甲离开A地的时间t(h)之间的函数关系的图象如图所示,根据图象提供的信息,有下列说法:①甲、乙同学都骑行了18km;②甲、乙同学同时到达B地;③甲停留前、后的骑行速度相同;④乙的骑行速度是
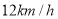 ;其中正确的说法是( )
;其中正确的说法是( )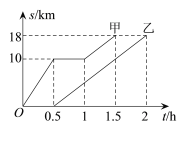
A. ①③B. ①④C. ②④D. ②③
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场购进一批 30 瓦的 LED 灯泡和普通白炽灯泡进行销售,其进价与标价如下表:
LED 灯泡
普通白炽灯泡
进价(元)
45
25
标价(元)
60
30

(1)该商场购进了 LED 灯泡与普通白炽灯泡共 300 个,LED 灯泡按标价进行销售,而普通 白炽灯泡打九折销售,当销售完这批灯泡后可获利 3 200 元,求该商场购进 LED 灯泡与 普通白炽灯泡的数量分别为多少个?
(2)由于春节期间热销,很快将两种灯泡销售完,若该商场计划再次购进这两种灯泡 120 个, 在不打折的情况下,请问如何进货,销售完这批灯泡时获利最多且不超过进货价的 30%, 并求出此时这批灯泡的总利润为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机沿东西方向的公路送旅客,如果约定向东为正,向西为负,当天的历史记录如下(单位:千米)
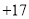 ,
, ,
, ,
,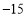 ,
,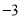 ,
,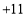 ,
, ,
, ,
,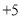 ,
,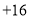
(1)出租车司机最后到达的地方在出发点的哪个方向?距出发点多远?
(2)出租车司机最远离出发点有多远?
(3)若汽车每千米耗油量为
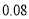 升,则这天共耗油多少升?
升,则这天共耗油多少升? -
科目: 来源: 题型:
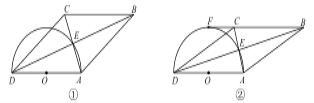
查看答案和解析>>【题目】四边形 ABCD 的对角线交于点 E,且 AE=EC,BE=ED,以 AD 为直径的半圆过点 E,圆心 为 O.
(1)如图①,求证:四边形 ABCD 为菱形;
(2)如图②,若 BC 的延长线与半圆相切于点 F,且直径 AD=6,求弧AE 的长.
相关试题

