【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.下列说法不正确的是( )

A.与∠1互余的角只有∠2B.∠A与∠B互余
C.∠1=∠BD.若∠A=2∠1,则∠B=30°
参考答案:
【答案】A
【解析】
根据直角三角形两锐角互余和等角或同角的余角相等对各选项分析判断后利用排除法求解.
解:A、∵∠ACB=90°,
∴∠1+∠2=90°,
∵CD⊥AB,
∴∠1+∠A=90°,
∴与∠1互余的角有∠2与∠A两个角,故本选项错误;
B、∵∠ACB=90°,
∴∠A+∠B=90°,
∴∠A与∠B互余,故本选项正确;
C、∠1+∠2=90°,∠2+∠B=90°,
∴∠1=∠B,故本选项正确;
D、∵∠A=2∠1=2∠B,
∴∠A+∠B=3∠B=90°,
解得∠B=30°,故本选项正确.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图像与反比例函数y=
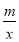 的图像交于点,A(n,3)和点B(1,-6),与y轴交于点C.
的图像交于点,A(n,3)和点B(1,-6),与y轴交于点C.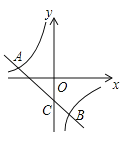
(1)求一次函数和反比例函数表达式;
(2)请直接写出关于x的不等式kx+b>
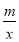 的解集;
的解集;(3)把点C绕着点O逆时针旋转90°,得到点
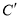 ,连接
,连接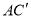 ,
,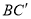 ,求△AB
,求△AB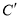 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线AC、BD相交于点O,E是OB的中点,过点B作BF∥AC交AE的延长线于点F,连接CF.

(1)求证:△AOE≌△FBE;
(2)求证:四边形BOCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。

其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成下列推理过程
已知:如图,BD⊥AC,EF⊥AC,点D、F分别是垂足,∠1=∠4.

试说明:∠ADG=∠C
解:∵BD⊥AC,EF⊥AC(已知)
∴∠2=90°∠3=90°(垂直的定义)
∴∠2=∠3(等量代换)
∴BD∥EF
∴∠4=∠5(两直线平行同位角相等)
∵∠1=∠4(已知)
∠1=∠5
∴DG∥CB(内错角相等两直线平行)
∴∠ADG=∠C
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校初三(1)班部分同学接受一次内容为“最适合自己的考前减压方式”的调查活动,收集整理数据后,老师将减压方式分为五类,并绘制了图1、图2两个不完整的统计图,请根据图中的信息解答下列问题.
(1)初三(1)班接受调查的同学共有多少名;
(2)补全条形统计图,并计算扇形统计图中的“体育活动C”所对应的圆心角度数;
(3)若喜欢“交流谈心”的5名同学中有三名男生和两名女生;老师想从5名同学中任选两名同学进行交流,直接写出选取的两名同学都是女生的概率.

-
科目: 来源: 题型:
查看答案和解析>>【题目】小明某天上午9时骑自行车离开家,15时回家,他有意描绘了离家的距离与时间的变化情况(如图所示).

(1)图象表示了哪两个变量的关系?
(2)10时,他离家多远?
(3)他到达离家最远的地方是什么时间?离家多远?
(4)他可能在哪段时间内休息,并吃午餐?
(5)他由离家最远的地方返回时的平均速度是多少?
相关试题

