【题目】如图,矩形ABCD的对角线AC、BD相交于点O,E是OB的中点,过点B作BF∥AC交AE的延长线于点F,连接CF.

(1)求证:△AOE≌△FBE;
(2)求证:四边形BOCF是菱形.
参考答案:
【答案】(1)见解析;(2)见解析
【解析】
(1)根据E是OB的中点得OE=BE,根据BF∥AC得∠AOE=∠FBE,∠OAE=∠BFE,进而根据“AAS”即可证得△AOE≌△FBE;
(2)由矩形ABCD可得AO=CO=BO,由△AOE≌△FBE可得AO=BF,进而可得CO=BF,根据BF∥AC,CO=BF可得四边形BOCF是平行四边形,再结合CO=BO即可得证.
证明:(1)∵E是OB的中点,
∴OE=BE,
∵BF∥AC,
∴∠AOE=∠FBE,∠OAE=∠BFE,
在△AOE与△FBE中,
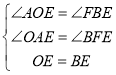
∴△AOE≌△FBE(AAS);
(2)∵矩形ABCD的对角线AC、BD相交于点O,
∴AO=CO=BO,
∵△AOE≌△FBE,
∴AO=BF,
∴CO=BF,
∵BF∥AC,CO=BF,
∴四边形BOCF是平行四边形,
又∵CO=BO,
∴四边形BOCF是菱形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是二次函数y=ax2+bx+c(a≠0)图象的一部分,对称轴是直线x=-2.关于下列结论:①ab<0;②b2-4ac>0;③25a-5b+c>0;④b-4a=0;⑤方程ax2+bx=0的两个根为x1=0,x2=-4,其中正确的结论有( )
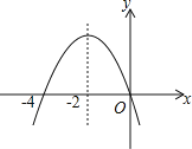
A. 2个 B. 3个
C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】出租车司机小张某天上午劳动线路是在南北走向的公路上进行的,如果规定向南为正,向北为负,他这天上午行车里程(单位:千米)如下:
 ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, ,
, .
.(1)将最后一名乘客送到目的地时,小张距上午出发时的出发点多远?在出发点的南边还是北边?
(2)若汽车耗油量为
 升/千米,这天上午汽车耗油多少升?
升/千米,这天上午汽车耗油多少升? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数y=kx+b的图像与反比例函数y=
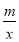 的图像交于点,A(n,3)和点B(1,-6),与y轴交于点C.
的图像交于点,A(n,3)和点B(1,-6),与y轴交于点C.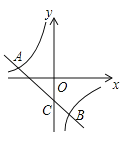
(1)求一次函数和反比例函数表达式;
(2)请直接写出关于x的不等式kx+b>
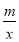 的解集;
的解集;(3)把点C绕着点O逆时针旋转90°,得到点
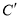 ,连接
,连接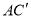 ,
,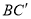 ,求△AB
,求△AB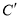 的面积.
的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】下图的转盘被划分成六个相同大小的扇形,并分别标上1,2,3,4,5,6这六个数字,指针停在每个扇形的可能性相等。四位同学各自发表了下述见解:
甲:如果指针前三次都停在了3号扇形,下次就一定不会停在3号扇形;
乙:只要指针连续转六次,一定会有一次停在6号扇形;
丙:指针停在奇数号扇形的概率与停在偶数号扇形的概率相等;
丁:运气好的时候,只要在转动前默默想好让指针停在6号扇形,指针停在6号扇形的可能性就会加大。

其中,你认为正确的见解有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D.下列说法不正确的是( )

A.与∠1互余的角只有∠2B.∠A与∠B互余
C.∠1=∠BD.若∠A=2∠1,则∠B=30°
-
科目: 来源: 题型:
查看答案和解析>>【题目】填空完成下列推理过程
已知:如图,BD⊥AC,EF⊥AC,点D、F分别是垂足,∠1=∠4.

试说明:∠ADG=∠C
解:∵BD⊥AC,EF⊥AC(已知)
∴∠2=90°∠3=90°(垂直的定义)
∴∠2=∠3(等量代换)
∴BD∥EF
∴∠4=∠5(两直线平行同位角相等)
∵∠1=∠4(已知)
∠1=∠5
∴DG∥CB(内错角相等两直线平行)
∴∠ADG=∠C
相关试题

