【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的图象刻画了“龟兔再次赛跑”的故事(![]() 表示乌龟从起点出发所行的时间,
表示乌龟从起点出发所行的时间,![]() 表示乌龟所行的路程,
表示乌龟所行的路程,![]() 表示兔子所行的路程).
表示兔子所行的路程).
①“龟兔再次赛跑”的路程为______米;
②兔子比乌龟晚出发______分钟;
③乌龟在途中休息了______分钟;
④乌龟的速度是______米/分;
⑤兔子的速度是______米/分;
⑥兔子在距起点______米处追上乌龟.

参考答案:
【答案】①1000;②40;③10;④20;⑤100;⑥750
【解析】
①由函数图像求得①“龟兔再次赛跑”的路程为1000米;
②由函数图像求得②兔子比乌龟晚出发40分钟;
③由函数图像求得③乌龟在途中休息了10分钟;
④由函数图像求得④乌龟跑完全程用了60分钟,从而可求其速度,
⑤由函数图像求得⑤兔子跑完全程用了10分钟,从而可求其速度,
⑥利用追击时间=追击路程÷速度差求得追击时间,从而求解.
解:①有函数图像可得:龟兔再次赛跑的路程为1000米
故答案为:1000;
②兔子比乌龟晚出发40分钟,
故答案为:40;
③乌龟在途中休息了10分钟,
故答案为:10;
④乌龟的速度为:1000÷50=20米/分,
故答案为:20;
⑤兔子的速度为:1000÷10=100米/分,
故答案为:100;
⑥兔子追上乌龟时离起点的距离为:20×30÷(100-20)×100=750米,
故答案为:750.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,点O在AC上,以OA为半径的⊙O交AB于点D,BD的垂直平分线交BC于点E,交BD于点F,连接DE.

(1)求证:直线DE是⊙O的切线;
(2)若AC=6,BC=8,OA=2,求线段AD和DE的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为4的正方形ABCD中,P是BC边上一动点(不与B、C两点重合),将△ABP沿直线AP翻折,点B落在点E处;在CD上取一点M,使得将△CMP沿直线MP翻折后,点C落在直线PE上的点F处,直线PE交CD于点N,连接AM、AN.

(1)若P为BC的中点,则sin∠CPM=________;
(2)求证:∠PAN的度数不变;
(3)当P在BC边上运动时,△ADM的面积是否存在最小值,若存在,请求出PB的长;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:小刚站在河边的
 点处,在河的对面(小刚的正北方向)的
点处,在河的对面(小刚的正北方向)的 处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树
处有一电线塔,他想知道电线塔离他有多远,于是他向正西方向走了30步到达一棵树 处,接着再向前走了30步到达
处,接着再向前走了30步到达 处,然后他左转
处,然后他左转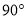 直行,当小刚看到电线塔、树与自己现处的位置
直行,当小刚看到电线塔、树与自己现处的位置 在一条直线时,他共走了140步.
在一条直线时,他共走了140步.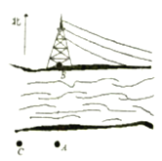
(1)根据题意,画出示意图;
(2)如果小刚一步大约50厘米,估计小刚在点
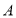 处时他与电线塔的距离,并说明理由.
处时他与电线塔的距离,并说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】问题:探究函数的图象与性质.
小华根据学习函数的经验,对函数的图象与性质进行了探究.下面是小华的探究过程,请补充完整:
在函数
 中,自变量
中,自变量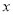 可以是任意实数;
可以是任意实数;(1)下表是
 与
与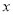 的几组对应值.
的几组对应值.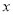
…
-3
-2
-1
0
1
2
3
…

…
1
0
-1
-2
-1
0
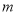
…
①
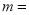 ______;
______;②若
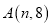 ,
,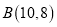 为该函数图象上不同的两点,则
为该函数图象上不同的两点,则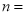 ______;
______;(2)如图,在平面直角坐标系
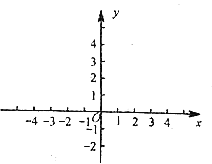
 中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;
中,描出以上表中各对对应值为坐标的点.并根据描出的点,画出该函数的图象;(3)根据函数图象可得函数的性质:
①该函数的最小值为______;
②再写出该函数一条性质____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+
 与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
与x轴交于点A、B(点A在点B的左侧),抛物线的顶点为C,直线AC交y轴于点D,D为AC的中点.
(1)如图1,求抛物线的顶点坐标;
(2)如图2,点P为抛物线对称轴右侧上的一动点,过点P作PQ⊥AC于点Q,设点P的横坐标为t,点Q的横坐标为m,求m与t的函数关系式;
(3)在(2)的条件下,如图3,连接AP,过点C作CE⊥AP于点E,连接BE、CE分别交PQ于F、G两点,当点F是PG中点时,求点P的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一坐标系中,一次函数y=﹣mx+n2与二次函数y=x2+m的图象可能是( )
A.
 B.
B.  C.
C.  D.
D. 
相关试题

