【题目】如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数y=![]() 在第一象限内的图象相交于点B(m,2).
在第一象限内的图象相交于点B(m,2).
(1)求该反比例函数的关系式;
(2)若直线y=x-2向上平移后与反比例函数y=![]() 在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.
在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.

参考答案:
【答案】(1) y=![]() (2). y=x+7.
(2). y=x+7.
【解析】试题分析:(1)设反比例解析式为y=![]() ,将B坐标代入直线y=x-2中求出m的值,确定出B坐标,将B的坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
,将B坐标代入直线y=x-2中求出m的值,确定出B坐标,将B的坐标代入反比例解析式中求出k的值,即可确定出反比例解析式;
(2)设平移后的直线交y轴于H,根据两平行线间的距离相等,可得C到AB的距离与H到AB的距离相等,根据等底等高的三角形的面积相等,可得b的值,根据待定系数法,可得答案.
解:(1)∵点B(m,2)在直线y=x-2上,
∴m-2=2,解得m=4,∴点B(4,2).
又∵点B(4,2)在反比例函数y=![]() 的图象上,
的图象上,
∴k=8,∴反比例函数的关系式为y=![]() .
.
(2)设平移后的直线对应的函数关系式为y=x+b,C点坐标为![]() .
.
∵△ABC的面积为18,∴4×![]() -
-![]() ×4×4-
×4×4-![]() ×(4-x)
×(4-x)![]() -
-![]() x
x![]() =18,
=18,
化简,得x2+7x-8=0,解得x1=-8,x2=1.
∵x>0,∴x=1,∴C点坐标为(1,8).
把C点坐标(1,8)代入y=x+b得:8=1+b,∴b=7.
∴平移后的直线对应的函数关系式为y=x+7.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上.

A.0B.1C.2D.3
-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高【 】
A.40% B.33.4% C.33.3% D.30%
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
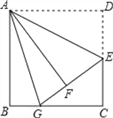
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
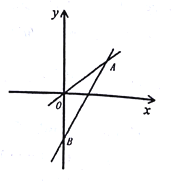
查看答案和解析>>【题目】如图,一次函数
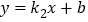 的图象与
的图象与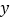 轴交于点
轴交于点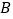 ,与正比例函数
,与正比例函数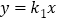 的图象相交于点
的图象相交于点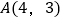 ,且
,且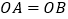 .
.
(1)分别求出这两个函数的解析式;
(2)求
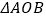 的面积;
的面积;(3)点
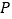 在
在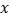 轴上,且
轴上,且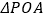 是等腰三角形,请直接写出点
是等腰三角形,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】我市从2018年1月1日开始,禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划最多投入8万元购进A、B两种型号的电动自行车共30辆,其中每辆B型电动自行车比每辆A型电动自行车多500元.用5万元购进的A型电动自行车与用6万元购进的B型电动自行车数量一样.
(1)求A、B两种型号电动自行车的进货单价;
(2)若A型电动自行车每辆售价为2800元,B型电动自行车每辆售价为3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.写出y与m之间的函数关系式;
(3)在(2)的条件下,该商店如何进货才能获得最大利润?此时最大利润是多少元?
-
科目: 来源: 题型:
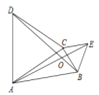
查看答案和解析>>【题目】如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为________。
相关试题

