【题目】我市从2018年1月1日开始,禁止燃油助力车上路,于是电动自行车的市场需求量日渐增多.某商店计划最多投入8万元购进A、B两种型号的电动自行车共30辆,其中每辆B型电动自行车比每辆A型电动自行车多500元.用5万元购进的A型电动自行车与用6万元购进的B型电动自行车数量一样.
(1)求A、B两种型号电动自行车的进货单价;
(2)若A型电动自行车每辆售价为2800元,B型电动自行车每辆售价为3500元,设该商店计划购进A型电动自行车m辆,两种型号的电动自行车全部销售后可获利润y元.写出y与m之间的函数关系式;
(3)在(2)的条件下,该商店如何进货才能获得最大利润?此时最大利润是多少元?
参考答案:
【答案】(1)A、B两种型号电动自行车的进货单价分别为2500元、3000元;(2)y=﹣200m+15000;(3)m=20时,y有最大值,最大值为11000元.
【解析】
(1)设A、B两种型号电动自行车的进货单价分别为x元(x+500)元,构建分式方程即可解决问题;
(2)根据总利润=A型的利润+B型的利润,列出函数关系式即可;
(3)利用一次函数的性质即可解决问题;
(1)设A、B两种型号电动自行车的进货单价分别为x元(x+500)元.
由题意:![]() ,
,
解得x=2500,
经检验:x=2500是分式方程的解.
答:A、B两种型号电动自行车的进货单价分别为2500元3000元.
(2)依题意,得:![]()
解得: ![]()
![]() y=(2800-2500)m+(3500-3000)(30-m)
y=(2800-2500)m+(3500-3000)(30-m)
=15000-200m
答:y与x之间的函数关系式为: y=15000-200m(![]() )
)
(3)设购进A型电动自行车m辆,
∵最多投入8万元购进A、B两种型号的电动自行车共30辆,
A、B两种型号电动自行车的进货单价分别为2500元、3000元,
∴2500m+3000(30﹣m)≤80000,
解得:m≥20,
∴m的取值范围是:20≤m≤30,
∵y=300m+500(30﹣m)=﹣200m+15000,
∵﹣200<0,
∴m=20时,y有最大值,最大值为11000元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
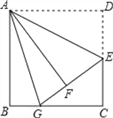
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数y=
 在第一象限内的图象相交于点B(m,2).
在第一象限内的图象相交于点B(m,2).(1)求该反比例函数的关系式;
(2)若直线y=x-2向上平移后与反比例函数y=
 在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.
在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一次函数
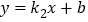 的图象与
的图象与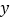 轴交于点
轴交于点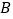 ,与正比例函数
,与正比例函数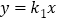 的图象相交于点
的图象相交于点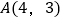 ,且
,且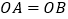 .
.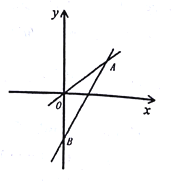
(1)分别求出这两个函数的解析式;
(2)求
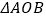 的面积;
的面积;(3)点
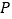 在
在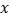 轴上,且
轴上,且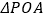 是等腰三角形,请直接写出点
是等腰三角形,请直接写出点 的坐标.
的坐标. -
科目: 来源: 题型:
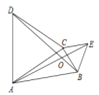
查看答案和解析>>【题目】如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图A、B分别为数轴上的两点,A点对应的数为-10 ,B点对应的数为90.

(1)请写出AB的中点M对应的数.
(2)现在有一只电子蚂蚁P从B点出发,以3个单位/秒的速度向左运动,同时另一只电子蚂蚁Q恰好从A点出发,以2个单位/秒的速度向右运动,设两只电子蚂蚁在数轴上的C点相遇,
①你知道经过几秒两只电子蚂蚁相遇?
②点C对应的数是多少?
③经过多长时间两只电子蚂蚁在数轴上相距10个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,一次函数y1=k1x+2的图象与反比例函数y2=
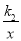 的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
的图象交于点A(4,m)和B(-8,-2),与y轴交于点C.
(1)k1=__________,k2=__________;
(2)根据函数图象可知,当y1>y2时,x的取值范围是____________;
(3)过点A作AD⊥x轴于点D,点P是反比例函数在第一象限的图象上一点.设直线OP与线段AD交于点E,当S四边形ODACS△ODE=31时,求点P的坐标.
相关试题

