【题目】如图,在△ABC中,∠C=90°,∠B=30°,以A为圆心,任意长为半径画弧分别交AB、AC于点M和N,再分别以M、N为圆心,大于MN的长为半径画弧,两弧交于点P,连结AP并延长交BC于点D,则下列说法中正确的个数是( )
①AD是∠BAC的平分线;②∠ADC=60°;③点D在AB的垂直平分线上.

A.0B.1C.2D.3
参考答案:
【答案】D
【解析】
由角平分线的作法可知AD是BAC的平分线,由直角三角形两锐角互余可知∠CAB=60°,从而可知∠BAD=30°,由此可将∠BAD=∠B=30°,从而得到AD=DB,根据到线段两端距离相等的点在线段的垂直平分线上可判断③;由三角形的外角的性质可知∠ADC=∠B+∠BAD可判断.
解:由角平分线的作法可知①正确;
∵∠C=90°,∠B=30°,
∴∠BAC=60°.
∵AD是∠BAC的平分线,
∴∠BAD=30°.
∴∠BAD=∠B=30°.
∴AD=DB.
∴点D在AB的垂直平分线上.
∴③正确.
∵∠ADC=∠B+∠BAD,
∴∠ADC=30°+30°=60°.
故②正确.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下列材料、并完成任务.
无限循环小数化分数
我们知道分数
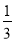 写出小数形式即
写出小数形式即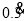 ,反过来,无限循环小数
,反过来,无限循环小数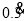 写成分数形式即
写成分数形式即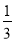 ,一般地,任何一个无限循环小数都可以写成分数形式.
,一般地,任何一个无限循环小数都可以写成分数形式.先以无限循环小数
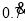 为例进行讨论.
为例进行讨论.设
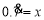 ,由
,由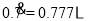 可知,
可知,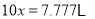 ,所以
,所以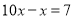 ,解方程,得
,解方程,得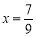 ,于是,得
,于是,得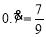 .
.再以无限循环小数
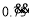 为例,做进一步的讨论.
为例,做进一步的讨论.无限循环小数
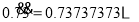 ,它的循环节有两位,类比上面的讨论可以想到如下做法.
,它的循环节有两位,类比上面的讨论可以想到如下做法.设
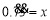 ,由
,由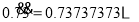 可知,
可知,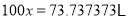 .
.所以
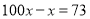 .解方程,得
.解方程,得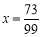 ,于是,
,于是,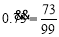 .
.类比应用(直接写出答案,不写过程)
①
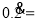 .②
.②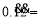 .③
.③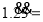 .
.能力提升
将
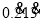 化为分数形式,写出过程.
化为分数形式,写出过程.拓展探究
①
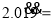 ;
;②比较大小
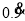 1(填“
1(填“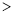 ”或“
”或“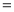 ”或“
”或“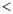 ”);
”);③若
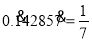 ,则
,则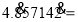 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在平面直角坐标系xOy中,抛物线m:y=﹣2x2﹣2x的顶点为C,与x轴两个交点为P,Q.现将抛物线m先向下平移再向右平移,使点C的对应点C′落在x轴上,点P的对应点P′落在y轴上,则下列各点的坐标不正确的是( )
A. C(﹣
 ,
, ) B. C′(1,0) C. P(﹣1,0) D. P′(0,﹣
) B. C′(1,0) C. P(﹣1,0) D. P′(0,﹣ )
) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图是药品研究所测得的某种新药在成人用药后,血液中的药物浓度y(微克/毫升)随用药后的时间x(小时)变化的图象(图象由线段OA与部分双曲线AB组成).并测得当y=a时,该药物才具有疗效.若成人用药4小时,药物开始产生疗效,且用药后9小时,药物仍具有疗效,则成人用药后,血液中药物浓度至少需要多长时间达到最大?

-
科目: 来源: 题型:
查看答案和解析>>【题目】某大型超市从生产基地购进一批水果,运输过程中质量损失10%,假设不计超市其他费用,如果超市要想至少获得20%的利润,那么这种水果的售价在进价的基础上应至少提高【 】
A.40% B.33.4% C.33.3% D.30%
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在边长为12的正方形ABCD中,E是边CD的中点,将△ADE沿AE对折至△AFE,延长EF交BC于点G.则BG的长为( )
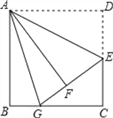
A. 5 B. 4 C. 3 D. 2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,直线y=x-2与y轴相交于点A,与反比例函数y=
 在第一象限内的图象相交于点B(m,2).
在第一象限内的图象相交于点B(m,2).(1)求该反比例函数的关系式;
(2)若直线y=x-2向上平移后与反比例函数y=
 在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.
在第一象限内的图象相交于点C,且△ABC的面积为18,求平移后的直线对应的函数关系式.
相关试题

