【题目】列方程组或不等式解应用题
现有![]() ,
,![]() 两种商品,买2件
两种商品,买2件![]() 商品和1件
商品和1件![]() 商品用了80元,买4件
商品用了80元,买4件![]() 商品和3件
商品和3件![]() 商品用了180元
商品用了180元
(1)求![]() ,
,![]() 两种商品每件各是多少元?
两种商品每件各是多少元?
(2)如果小亮准备购买![]() ,
,![]() 两种商品共10件,总费用不超过260元,至少买多少件
两种商品共10件,总费用不超过260元,至少买多少件![]() 商品?
商品?
参考答案:
【答案】(1)A、B两种商品每件各是30元20元;(2)至少买4件B商品.
【解析】
(1)设A种商品每件![]() 元,B件商品每件
元,B件商品每件![]() 元,由两种商品的总价分别为
元,由两种商品的总价分别为![]() 元和
元和![]() 元建立方程组求出其解即可;
元建立方程组求出其解即可;
(2)设小亮最多可以买![]() 件B商品,则购买A商品
件B商品,则购买A商品![]() 件,由总费用不超过
件,由总费用不超过![]() 元建立不等式求出其解即可.
元建立不等式求出其解即可.
(1)设![]() 、
、![]() 两种商品每件各是
两种商品每件各是![]() 元、
元、![]() 元,由题意得:
元,由题意得:
![]()
解得:![]()
答:![]() 、
、![]() 两种商品每件各是30元20元。
两种商品每件各是30元20元。
(2)设买![]() 种商品
种商品![]() 件,由题意得:
件,由题意得:
![]()
答:至少买4件![]() 商品。
商品。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC.
(1)求证:△BFO≌△DEO;
(2)若EF平分∠AEC,试判断四边形AFCE的形状,并证明.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某校开展了“互助、平等、感恩、和谐、进取”主题班会活动,活动后,就活动的
 个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:
个主题进行了抽样调查(每位同学只选最关注的一个),根据调查结果绘制了两幅不完整的统计图.根据图中提供的信息,解答下列问题:(1)这次调查的学生共有多少名?
(2)请将条形统计图补充完整,并在扇形统计图中计算出“进取”所对应的圆心角的度数.
(3)如果要在这
 个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
个主题中任选两个进行调查,根据(2)中调查结果,用树状图或列表法,求恰好选到学生关注最多的两个主题的概率(将互助、平等、感恩、和谐、进取依次记为A、B、C、D、E).
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:

(说明:成绩80分及以上为优秀,
 分为良好,
分为良好, 分为合格,60分以下为不合格)
分为合格,60分以下为不合格)b.甲校成绩在
 这一组的是:70707071727373737475767778
这一组的是:70707071727373737475767778c.甲、乙两校成绩的平均分、中位数、众数如下:
学校
平均分(单位:分)
中位数(单位:分)
众数(单位:分)
甲
74.2

85
乙
73.5
76
84
根据以上信息,回答下列问题:
(1)上表中n的值为_____.
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是___校的学生(填“甲”或“乙”),请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD的对角线相交于点O,分别过点C、D作CE∥BD、DE∥AC,CE、DE交于点E.

(1)求证:四边形OCED是菱形.
(2)将矩形ABCD改为菱形ABCD,其余条件不变,连结OE.若AC=10,BD=24,则OE的长为____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:
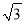 ≈1.732)
≈1.732)
相关试题

