【题目】在ABCD中,对角线AC、BD相交于O,EF过点O,且AF⊥BC.
(1)求证:△BFO≌△DEO;
(2)若EF平分∠AEC,试判断四边形AFCE的形状,并证明.

参考答案:
【答案】四边形AFCE是正方形.
【解析】
试题分析:根据平行四边形的性质和平行线性质得出OA=OC,∠OAE=∠OCF,证△AOE≌△COF,推出OE=OF,即可得出四边形是矩形.
试题解析:(1)证明:∵四边形ABCD是平行四边形,
∴OB=OD,AD∥BC,AD=BC,
∴∠OBF=∠ODE,
在△BFO和△DEO中, ,
,
∴△BFO≌△DEO(ASA);
(2)解:四边形AFCE是正方形;理由如下:
∵△BFO≌△DEO,
∴BF=DE,
∴CF=AE,
∵AD∥BC,
∴四边形AFCE是平行四边形,
又∵AF⊥BC,
∴∠AFC=90°,
∴四边形AFCE是矩形,
∵EF平分∠AEC,
∴∠AEF=∠CEF,
∵AD∥BC,
∴∠AEF=∠CFE,
∴∠CEF=∠CFE,
∴CE=CF,
∴四边形AFCE是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(结果保留π)
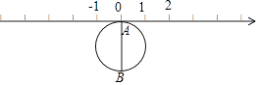
(1)把圆片沿数轴向左滚动1周,点A到达数轴上点C的位置,点C表示的数是数(填“无理”或“有理”),这个数是;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3 ①第几次滚动后,A点距离原点最近?第几次滚动后,A点距离原点最远?
②当圆片结束运动时,A点运动的路程共有多少?此时点A所表示的数是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一次函数y=(k﹣2)x+1的图象经过一、二、三象限,那么常数k的取值范围是______.
-
科目: 来源: 题型:
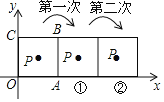
查看答案和解析>>【题目】如图,把正方形铁片OABC置于平面直角坐标系中,顶点A的坐标为(3,0),点P(1,2)在正方形铁片上,将正方形铁片绕其右下角的顶点按顺时针方向依次旋转90°,第一次旋转至图①位置,第二次旋转至图②位置…,则正方形铁片连续旋转2017次后,点P的坐标为_____________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解:若A、B、C为数轴上三点,若点C到A的距离是点C到B的距离2倍,我们就称点C是点是【A,B】的好点.
(1)如图1,点A表示的数为﹣1,点B表示的数为2.表示1的点C到点A的距离是2,到点B的距离是1,那么点C是【A,B】的好点; 又如,表示0的点D到点A的距离是1,到点B的距离是2,那么点D【A,B】的好点,但点D【B,A】的好点.(请在横线上填是或不是)知识运用:
(2)如图2,M、N为数轴上两点,点M所表示的数为4,点N所表示的数为﹣2.数所表示的点是【M,N】的好点;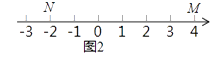
(3)如图3,A、B为数轴上两点,点A所表示的数为﹣20,点B所表示的数为40.现有一只电子蚂蚁P从点B出发,以4个单位每秒的速度向左运动,到达点A停止.当经过秒时,P、A和B中恰有一个点为其余两点的好点?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知y+3与x+2成正比例,且当x=3时,y=7.
(1)写出y与x之间的函数关系式;
(2)当x=﹣1时,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A,B,C三点,分别代表﹣30,﹣10,10,两只电子蚂蚁甲,乙分别从A,C两点同时相向而行,甲的速度为4个单位/秒,乙的速度为6个单位/秒.
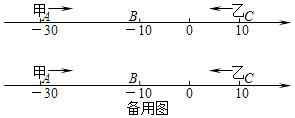
(1)甲,乙在数轴上的哪个点相遇?
(2)多少秒后,甲到A,B,C的距离和为48个单位?
(3)在甲到A,B,C的距离和为48个单位时,若甲调头并保持速度不变,则甲,乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由.
相关试题

