【题目】如图,矩形ABCD的对角线相交于点O,分别过点C、D作CE∥BD、DE∥AC,CE、DE交于点E.

(1)求证:四边形OCED是菱形.
(2)将矩形ABCD改为菱形ABCD,其余条件不变,连结OE.若AC=10,BD=24,则OE的长为____.
参考答案:
【答案】(1)见解析;(2)13
【解析】
(1)首先由平行判定四边形OCED是平行四边形,然后由矩形性质得出OC=OD,即可判定四边形OCED是菱形;
(2)首先由平行判定四边形OCED是平行四边形,然后由菱形性质得出AC⊥BD,AD=CD,即可判定四边形OCED是矩形,再利用勾股定理即可得解.
(1)∵DE∥AC、CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是矩形,
∴AC=BD,![]() ,
,![]() .
.
∴OC=OD.
∴四边形OCED是菱形.
(2)∵DE∥AC、CE∥BD,
∴四边形OCED是平行四边形.
∵四边形ABCD是菱形,
∴AC⊥BD,AD=CD
∴∠COD=90°
∴四边形OCED是矩形
∴OE=CD
∵AC=10,BD=24,
∴OD=12,OC=5
∴OE=CD=![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,一次函数y=kx+b(k≠0)的图象与反比例函数
 (m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.
(m≠0)的图象交于A、B两点,与x轴交于C点,点A的坐标为(n,6),点C的坐标为(﹣2,0),且tan∠ACO=2.(1)求该反比例函数和一次函数的解析式;
(2)求点B的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】列方程组或不等式解应用题
现有
 ,
, 两种商品,买2件
两种商品,买2件 商品和1件
商品和1件 商品用了80元,买4件
商品用了80元,买4件 商品和3件
商品和3件 商品用了180元
商品用了180元(1)求
 ,
, 两种商品每件各是多少元?
两种商品每件各是多少元?(2)如果小亮准备购买
 ,
, 两种商品共10件,总费用不超过260元,至少买多少件
两种商品共10件,总费用不超过260元,至少买多少件 商品?
商品? -
科目: 来源: 题型:
查看答案和解析>>【题目】为了调查学生对垃圾分类及投放知识的了解情况,从甲、乙两校各随机抽取40名学生进行了相关知识测试,获得了他们的成绩(百分制),并对数据(成绩)进行了整理、描述和分析.下面给出了部分信息.
a.甲、乙两校40名学生成绩的频数分布统计表如下:

(说明:成绩80分及以上为优秀,
 分为良好,
分为良好, 分为合格,60分以下为不合格)
分为合格,60分以下为不合格)b.甲校成绩在
 这一组的是:70707071727373737475767778
这一组的是:70707071727373737475767778c.甲、乙两校成绩的平均分、中位数、众数如下:
学校
平均分(单位:分)
中位数(单位:分)
众数(单位:分)
甲
74.2

85
乙
73.5
76
84
根据以上信息,回答下列问题:
(1)上表中n的值为_____.
(2)在此次测试中,某学生的成绩是74分,在他所属学校排在前20名,由表中数据可知该学生是___校的学生(填“甲”或“乙”),请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,MN表示某引水工程的一段设计路线,从点M到点N的走向为北偏西30°,在点M的北偏西60°方向上有一点A,以点A为圆心,以500米为半径的圆形区域为居民区,取MN上另一点B,测得BA的方向为北偏西75°.已知MB=400米,若不改变方向,则输水路线是否会穿过居民区?请通过计算说明理由.(参考数据:
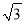 ≈1.732)
≈1.732)
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读下面材料并解决问题
我们在分析解决某些数学问题时,经常要比较两个数或代数式的大小而解决问题的策略般要进行一定的转化,其中“求差法”就是常用的方法之一,所谓“求差法”:就是通过求差、变形,并利用差的符号来确定它们的大小,即要比较代数式
 的大小,只要求出它们的差
的大小,只要求出它们的差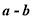 ,若
,若 ,则
,则 ;若
;若 ,则
,则 .若
.若 ,则
,则 ,
,请你用“求差法”解决以下问题
(1)若P=m2-2m-3,Q=m2-2m-1,比较
 的大小关系;
的大小关系;(2)制作某产品有两种用料方案方案一:用3块
 型钢板,用7块
型钢板,用7块 型钢板;方案二:用2块
型钢板;方案二:用2块 型钢板,用8块
型钢板,用8块 型钢板;
型钢板; 型钢板的面积比
型钢板的面积比 型钢板的面积大,设每块
型钢板的面积大,设每块 型钢板的面积为
型钢板的面积为 ,每块B型钢板的面积为
,每块B型钢板的面积为 ,从省料角度考虑,应选哪种方案?
,从省料角度考虑,应选哪种方案?(3)试比较图1和图2中两个矩形周长
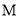 、
、 的大小.
的大小.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(感知)如图①,AC是菱形ABCD的对角线,∠B=60°,E、F分别是边BC、CD上的中点,连结AE、EF、AF.若AC=2,则CE+CF的长为_____.
(探究)如图②,在菱形ABCD中,∠B=60°.E是边BC上的点,连结AE,作∠EAF=60°,边AF交边CD于点F,连结EF.若BC=2,求CE+CF的长.
(应用)在菱形ABCD中,∠B=60°.E是边BC延长线上的点,连结AE,作∠EAF=60°,边AF交边CD延长线于点F,连结EF.若BC=2,EF⊥BC时,借助图③直接写出△AEF的周长.

相关试题

