【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 . 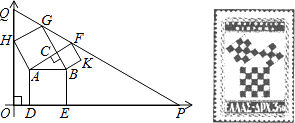
参考答案:
【答案】(7 ![]() +6,0)
+6,0)
【解析】延长BA交QR于点M,连接AR,AP,
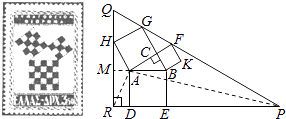
在△ABC与△GFC中,
![]()
![]()
![]()
![]()
![]()
又∵ ![]()
![]()
![]()
![]()
![]()
∴△QHG是等边三角形.
![]()
则 ![]()
在 ![]() 中,
中, ![]()
在 ![]() 中,
中, ![]()
![]()
![]()
![]()
∴点P的坐标为 ![]()
所以答案是: ![]()
【考点精析】关于本题考查的锐角三角函数的定义,需要了解锐角A的正弦、余弦、正切、余切都叫做∠A的锐角三角函数才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知直线l1、l2、l3互相平行,直线l1与l2的距离是4cm,直线l2与l3的距离是6cm,那么直线l1与l3的距离是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】为从甲、乙两名射击运动员中选出一人参加市锦标赛,特统计了他们最近10次射击训练的成绩,其中,他们射击的平均成绩都为8.9环,方差分别是S甲2=0.8,S乙2=1.3,从稳定性的角度来看的成绩更稳定.(填“甲”或“乙”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中, ,
, ,点
,点 是这个菱形内部或边上的一点,若以
是这个菱形内部或边上的一点,若以 为顶点的三角形是等腰三角形,则
为顶点的三角形是等腰三角形,则 ,
, (
( ,
, 两点不重合)两点间的最短距离为 cm.
两点不重合)两点间的最短距离为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,把解表示在数轴上,并写出该不等式组的非负整数解.
,把解表示在数轴上,并写出该不等式组的非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC , ∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF .
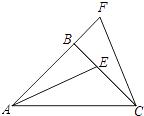
(1)求证:△ABE≌△CBF;
(2)若∠BAE=25°,求∠ACF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
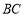 是
是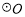 的直径,点
的直径,点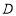 为
为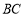 延长线上的一点,点
延长线上的一点,点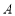 为圆上一点,且
为圆上一点,且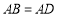 ,
,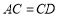 .
.(1)求证:
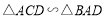 ;
;(2)求证:
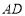 是
是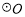 的切线.
的切线.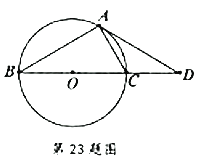
相关试题

