【题目】如图,△ABC中,AB=BC , ∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF . 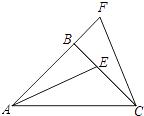
(1)求证:△ABE≌△CBF;
(2)若∠BAE=25°,求∠ACF的度数.
参考答案:
【答案】
(1)解:在 ![]() 与
与 ![]() 中,
中,
![]()
![]()
(2)解: ![]()
![]()
![]()
![]()
![]()
【解析】(1)根据题目中的条件直接利用HL判断出△ABE≌△CBF;
(2)根据全等三角形对应角相等得出∠BAE=∠BCF=25![]() ,根据等腰直角三角形的性质得出ACB=45
,根据等腰直角三角形的性质得出ACB=45![]() ,最后根据角的和差算出答案。
,最后根据角的和差算出答案。
【考点精析】利用等腰直角三角形和全等三角形的性质对题目进行判断即可得到答案,需要熟知等腰直角三角形是两条直角边相等的直角三角形;等腰直角三角形的两个底角相等且等于45°;全等三角形的对应边相等; 全等三角形的对应角相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在菱形
 中,
中, ,
, ,点
,点 是这个菱形内部或边上的一点,若以
是这个菱形内部或边上的一点,若以 为顶点的三角形是等腰三角形,则
为顶点的三角形是等腰三角形,则 ,
, (
( ,
, 两点不重合)两点间的最短距离为 cm.
两点不重合)两点间的最短距离为 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 .
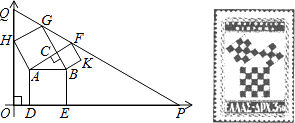
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,把解表示在数轴上,并写出该不等式组的非负整数解.
,把解表示在数轴上,并写出该不等式组的非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知
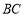 是
是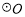 的直径,点
的直径,点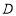 为
为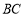 延长线上的一点,点
延长线上的一点,点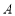 为圆上一点,且
为圆上一点,且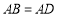 ,
,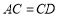 .
.(1)求证:
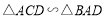 ;
;(2)求证:
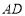 是
是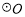 的切线.
的切线.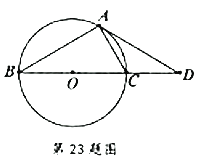
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x,3)和B(4,y)关于y轴对称,则(x+y)2014的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D , BC=CE .
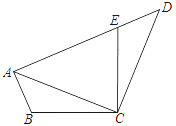
(1)求证:AC=CD;
(2)若AC=AE , 求∠DEC的度数.
相关试题

