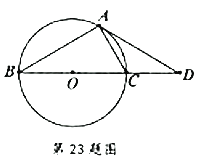
【题目】如图,已知![]() 是
是![]() 的直径,点
的直径,点![]() 为
为![]() 延长线上的一点,点
延长线上的一点,点![]() 为圆上一点,且
为圆上一点,且![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() 是
是![]() 的切线.
的切线.
参考答案:
【答案】(1)证明见解析(2)证明见解析.
【解析】
试题分析:(1)根据等腰三角形的性质得到∠CAD=∠B,由于∠D=∠D,于是得到△ACD∽△BAD;
(2)连接OA,根据的一句熟悉的性质得到∠B=∠OAB,得到∠OAB=∠CAD,由BC是⊙O的直径,得到∠BAC=90°即可得到结论.
试题解析:(1)∵AB=AD,
∴∠B=∠D,
∵AC=CD,
∴∠CAD=∠D,
∴∠CAD=∠B,
∵∠D=∠D,
∴△ACD∽△BAD;
(2)连接OA,

∵OA=OB,
∴∠B=∠OAB,
∴∠OAB=∠CAD,
∵BC是⊙O的直径,
∴∠BAC=90°,
∴OA⊥AD,
∴AD是⊙O的切线.
-
科目: 来源: 题型:
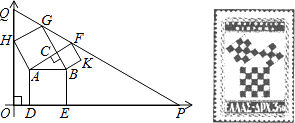
查看答案和解析>>【题目】勾股定理有着悠久的历史,它曾引起很多人的兴趣,1955年希腊发型了二枚以勾股图为背景的邮票.所谓勾股图是指以直角三角形的三边为边向外作正方形构成,它可以验证勾股定理.在如图的勾股图中,已知∠ACB=90°,∠BAC=30°,AB=4.作△PQO使得∠O=90°,点Q在在直角坐标系y轴正半轴上,点P在x轴正半轴上,点O与原点重合,∠OQP=60°,点H在边QO上,点D、E在边PO上,点G、F在边PQ上,那么点P坐标为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式组
 ,把解表示在数轴上,并写出该不等式组的非负整数解.
,把解表示在数轴上,并写出该不等式组的非负整数解. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=BC , ∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF .
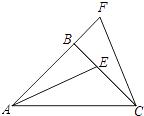
(1)求证:△ABE≌△CBF;
(2)若∠BAE=25°,求∠ACF的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知点A(x,3)和B(4,y)关于y轴对称,则(x+y)2014的值为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知:在四边形ABCD中,点E在AD上,∠BCE=∠ACD=90°,∠BAC=∠D , BC=CE .
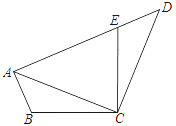
(1)求证:AC=CD;
(2)若AC=AE , 求∠DEC的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A.b3b3=2b3
B.(a+2)(a﹣2)=a2﹣4
C.(ab2)3=ab6
D.(8a﹣7b)﹣(4a﹣5b)=4a﹣12b
相关试题

