【题目】已知一次函数![]() 和反比例函数
和反比例函数![]() .
.
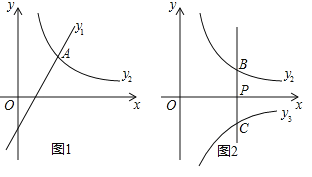
![]() 如图1,若
如图1,若![]() ,且函数
,且函数![]() 、
、![]() 的图象都经过点
的图象都经过点![]() .求m,k的值;
.求m,k的值;
![]() 如图2,过点
如图2,过点![]() 作y轴的平行线l与函数
作y轴的平行线l与函数![]() 的图象相交于点B,与反比例函数
的图象相交于点B,与反比例函数![]() 的图象相交于点C.
的图象相交于点C.
![]() 若
若![]() ,直线l与函数
,直线l与函数![]() 的图象相交点
的图象相交点![]() 当点B、C、D中的一点到另外两点的距离相等时,求
当点B、C、D中的一点到另外两点的距离相等时,求![]() 的值;
的值;
![]() 过点B作x轴的平行线与函数
过点B作x轴的平行线与函数![]() 的图象相交与点
的图象相交与点![]() 当
当![]() 的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
参考答案:
【答案】(1)m=12,k=2;(2)①m-n=1或m-n=4;②k=1,定值d=1
【解析】
(1)将点A的坐标代入一次函数表达式即可求解,将点A的坐标代入反比例函数表达式,即可求解;
(2)①BD=2+n﹣m,BC=m﹣n,DC=2+n﹣n=2,由BD=BC或BD=DC或BC=CD得:m﹣n=1或0或2,即可求解;
②点E的坐标为(![]() ,m),d=BC+BE=m﹣n+(1﹣
,m),d=BC+BE=m﹣n+(1﹣![]() )=1+(m﹣n)(1﹣
)=1+(m﹣n)(1﹣![]() ),即可求解.
),即可求解.
解:(1)当n=﹣2时,y1=kx﹣2,
将点A(3,4)代入一次函数y1=kx﹣2
得:3k﹣2=4,
解得:k=2,
将点A(3,4)代入反比例函数得:m=3×4=12;
∴m=12,k=2;
(2)①当x=1时,点D、B、C的坐标分别为(1,2+n)、(1,m)、(1,n),
则BD=|2+n﹣m|,BC=m﹣n,DC=2+n﹣n=2
则BD=BC或BD=DC或BC=CD,
即:|2+n﹣m|=m﹣n或|2+n﹣m|=2或m﹣n=2,
即:m﹣n=1或0或2或4,
当m﹣n=0时,m=n与题意不符,
点D不能在C的下方,即BC=CD也不存在,n+2>n,故m﹣n=2不成立,
故m﹣n=1或m﹣n=4;
②点E的横坐标为:![]() ,
,
当点E在点B左侧时,
d=BC+BE=m﹣n+(1﹣![]() )=1+(m﹣n)(1﹣
)=1+(m﹣n)(1﹣![]() ),
),
m﹣n的值取不大于1的任意数时,d始终是一个定值,
当1﹣![]() =0时,此时k=1,从而d=1.
=0时,此时k=1,从而d=1.
当点E在点B右侧时,
同理BC+BE=(m﹣n)(1+![]() )﹣1,
)﹣1,
当1+![]() =0,k=﹣1时,(不合题意舍去)
=0,k=﹣1时,(不合题意舍去)
故k=1,d=1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为应对越来越复杂的交通状况,某城市对其道路进行拓宽改造,工程队在工作了一段时间后,因雨被迫停工几天,随后工程队加快了施工进度,按时完成了拓宽改造任务.下面能反映该工程尚未改造的道路
 (米)与时间
(米)与时间 (天)的关系的大致图象是( )
(天)的关系的大致图象是( )A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】对称轴与 y轴平行且经过原点O的抛物线也经过A(2,m),B(4,m),若△AOB的面积为4,则抛物线的解析式为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探究函数y=x+
 的图象与性质】
的图象与性质】(1)函数y=x+
 的自变量x的取值范围是________;
的自变量x的取值范围是________;(2)下列四个函数图象中,函数y=x+
 的图象大致是________;
的图象大致是________;
(3)对于函数y=x+
 ,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
,求当x>0时,y的取值范围.请将下列的求解过程补充完整.解:∵x>0,∴y=x+
 =(
=( )2+
)2+ =
= +________.
+________.∵
 ≥0,∴y≥________.
≥0,∴y≥________.【拓展运用】
(4)若函数y=
 ,求y的取值范围.
,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(﹣1,0),C(﹣4,3).
(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;(其中A1、B1、C1分别是A、B、C的对应点,不写画法.)
(2)写出点A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
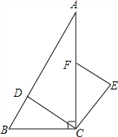
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边三角形
 的高为6,在这个三角形所在的平面内有一个点
的高为6,在这个三角形所在的平面内有一个点 ,若点
,若点 到
到 的距离是1,点
的距离是1,点 到
到 的距离是2,则点
的距离是2,则点 到
到 的最小距离与最大距离分别是_______.
的最小距离与最大距离分别是_______.
相关试题

