【题目】如图,在Rt△ABC中,∠ACB=90°,点D、F分别在AB、AC上,CF=CB,连接CD,将线段CD绕点C按顺时针方向旋转90°后得CE,连接EF.
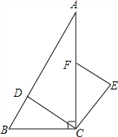
(1)求证:△BCD≌△FCE;
(2)若EF∥CD,求∠BDC的度数.
参考答案:
【答案】详见解析.
【解析】试题分析:(1)、根据旋转图形的性质可得:CD=CE,∠DCE=90°,根据∠ACB=90°得出∠BCD=90°-∠ACD=∠FCE,结合已知条件得出三角形全等;(2)、根据全等得出∠BDC=∠E,∠BCD=∠FCE,从而得出∠DCE=90°,然后根据EF∥CD得出∠BDC=90°.
试题解析:(1)、∵将线段CD绕点C按顺时针方向旋转90°后得CE,
∴CD=CE,∠DCE=90°,
∵∠ACB=90°,
∴∠BCD=90°-∠ACD=∠FCE,
在△BCD和△FCE中, CB=CF
∵BCD=∠FCE,CD=CE,CB=CF,∠BCD=∠FCE
∴△BCD≌△FCE(SAS).
(2)、由(1)可知△BCD≌△FCE,
∴∠BDC=∠E,∠BCD=∠FCE,
∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°,
∵EF∥CD,
∴∠E=180°-∠DCE=90°,
∴∠BDC=90°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】【探究函数y=x+
 的图象与性质】
的图象与性质】(1)函数y=x+
 的自变量x的取值范围是________;
的自变量x的取值范围是________;(2)下列四个函数图象中,函数y=x+
 的图象大致是________;
的图象大致是________;
(3)对于函数y=x+
 ,求当x>0时,y的取值范围.请将下列的求解过程补充完整.
,求当x>0时,y的取值范围.请将下列的求解过程补充完整.解:∵x>0,∴y=x+
 =(
=( )2+
)2+ =
= +________.
+________.∵
 ≥0,∴y≥________.
≥0,∴y≥________.【拓展运用】
(4)若函数y=
 ,求y的取值范围.
,求y的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
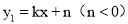 和反比例函数
和反比例函数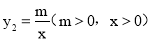 .
.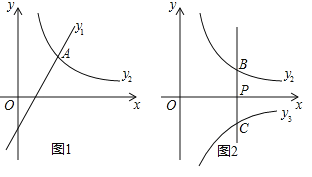
 如图1,若
如图1,若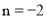 ,且函数
,且函数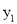 、
、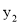 的图象都经过点
的图象都经过点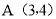 .求m,k的值;
.求m,k的值;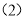 如图2,过点
如图2,过点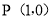 作y轴的平行线l与函数
作y轴的平行线l与函数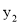 的图象相交于点B,与反比例函数
的图象相交于点B,与反比例函数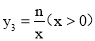 的图象相交于点C.
的图象相交于点C. 若
若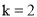 ,直线l与函数
,直线l与函数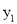 的图象相交点
的图象相交点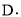 当点B、C、D中的一点到另外两点的距离相等时,求
当点B、C、D中的一点到另外两点的距离相等时,求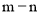 的值;
的值;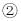 过点B作x轴的平行线与函数
过点B作x轴的平行线与函数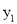 的图象相交与点
的图象相交与点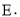 当
当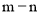 的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d.
的值取不大于1的任意实数时,点B、C间的距离与点B、E间的距离之和d始终是一个定值.求此时k的值及定值d. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系xOy中,A(-1,5),B(﹣1,0),C(﹣4,3).
(1)在图中画出△ABC关于y轴对称的图形△A1B1C1;(其中A1、B1、C1分别是A、B、C的对应点,不写画法.)
(2)写出点A1、B1、C1的坐标;
(3)求出△A1B1C1的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等边三角形
 的高为6,在这个三角形所在的平面内有一个点
的高为6,在这个三角形所在的平面内有一个点 ,若点
,若点 到
到 的距离是1,点
的距离是1,点 到
到 的距离是2,则点
的距离是2,则点 到
到 的最小距离与最大距离分别是_______.
的最小距离与最大距离分别是_______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 、
、 、
、 分别在
分别在 、
、 、
、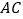 上,且
上,且 ,
, ,下面写出了说明“
,下面写出了说明“ ”的过程,请填空:
”的过程,请填空:
∵
 ,
,
∴
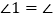 _______,
_______, ________.(________________________)
________.(________________________)∵

∴
 ___________,(________________________)
___________,(________________________)∵

∴
 ___________,(________________________)
___________,(________________________)∴
 .(等量代换)
.(等量代换)∵
 (平角定义)
(平角定义)∴
 (等量代换)
(等量代换) -
科目: 来源: 题型:
查看答案和解析>>【题目】某商场为了吸引顾客,设立了一个可以自由转动的转盘,如图所示,并规定:顾客消费200元(含200元)以上,就能获得一次转动转盘的机会,如果转盘停止后,指针正好对准九折、八折、七折区域,顾客就可以获得此项优惠,如果指针恰好在分割线上时,则需重新转动转盘.
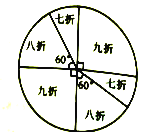
(1)某顾客正好消费220元,他转一次转盘,他获得九折、八折、七折优惠的概率分别是多少?
(2)某顾客消费中获得了转动一次转盘的机会,实际付费168元,请问他消费所购物品的原价应为多少元.
相关试题

