【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.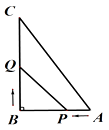
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
参考答案:
【答案】
(1)解:设t秒后,△PBQ的面积等于4cm2 ,
则列方程为:(5-t)×2t× ![]() =4,
=4,
解得t1=1,t2=4(舍),
答:1秒后,△PBQ的面积等于4cm2.
(2)解:设x秒后,△PBQ中PQ的长度等于5cm,
列方程为:(5-x)2+(2x)2=52 ,
解得x1=0(舍),x2=2,
答:2秒后,△PBQ中PQ的长度等于5cm。
(3)解:设面积为Scm2 , 时间为t,
则S=(5-t)×2t× ![]() =-t2+5t,
=-t2+5t,
当t=2.5时,面积最大.
【解析】(1)设t秒后,△PBQ的面积等于4cm2 , 根据题意PA=t ,BP=5-t ,BQ=2t ,根据三角形的面积公式及三角形的面积等于4,列出方程,求解并检验即可;
(2)设x秒后,△PBQ中PQ的长度等于5cm,根据题意PA=x ,BP=5-tx,BQ=2x ,根据勾股定理得出方程,求解并检验即可;
(3)设面积为Scm2 , 时间为t,根据三角形的面积公式得出S与t的函数解析式,从而得出次函数是S与t的二次函数,然后利用顶点坐标公式得出当t=2.5时,面积最大.
-
科目: 来源: 题型:
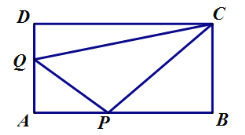
查看答案和解析>>【题目】如图,在矩形
 中,
中, ,
,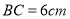 ,点
,点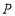 沿
沿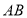 边从点
边从点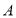 开始向点
开始向点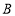 以
以 秒的速度移动;点
秒的速度移动;点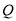 沿
沿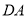 边从点
边从点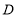 开始向点
开始向点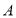 以
以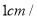 秒的速度移动,如果
秒的速度移动,如果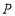 、
、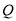 同时出发,用
同时出发,用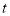 (秒)表示移动的时间(
(秒)表示移动的时间(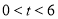 ).
).
(1)当
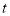 为何值时,
为何值时,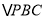 为等腰直角三角形.
为等腰直角三角形.(2)求当移动到
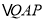 为等腰直角三角形时斜边
为等腰直角三角形时斜边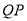 的长.
的长. -
科目: 来源: 题型:
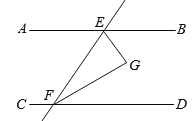
查看答案和解析>>【题目】如图,直线AB∥CD,直线AB、CD被直线EF所截,EG平分∠BEF,FG平分∠DFE,
(1)若∠AEF=50°,求∠EFG的度数.
(2)判断EG与FG的位置关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某童装专卖店在销售中发现,一款童装每件进价为80元,销售价为120元时,每天可售出20件,为了迎接“十一”国庆节,商店决定采取适当的降价措施,以扩大销售量,增加利润,经市场调查发现,如果每件童装降价1元,那么平均可多售出2件.
(1)设每件童装降价x元时,每天可销售件,每件盈利元;(用x的代数式表示)
(2)每件童装降价多少元时,平均每天赢利1200元.
(3)要想平均每天赢利2000元,可能吗?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在 ABCD中,CD=2AD,BE⊥AD于点E,F为DC的中点,连结EF、BF,下列结论:①∠ABC=2∠ABF;②EF=BF;③S四边形DEBC=2S△EFB;④∠CFE=3∠DEF,其中正确结论的个数共有( ).

A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知菱形ABCD的两条对角线分别为6和8,M、N分别是边BC、CD的中点,P是对角线BD上一点,则PM+PN的最小值=___.

-
科目: 来源: 题型:
查看答案和解析>>【题目】[阅读]
在平面直角坐标系中,以任意两点P( x1,y1)、Q(x2,y2)为端点的线段中点坐标为(
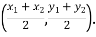 ,
,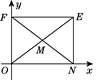 ).
).[运用]
(1)如图,矩形ONEF的对角线相交于点M,ON、OF分别在x轴和y轴上,O为坐标原点,点E的坐标为(4,3),则点M的坐标为 .
(2)在直角坐标系中,有A(﹣1,2),B(3,1),C(1,4)三点,另有一点D与点A、B、C构成平行四边形的顶点,求点D的坐标.

相关试题

