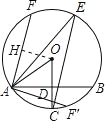
【题目】如图,AB是⊙O的一条弦,且AB=![]() .点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
.点C,E分别在⊙O上,且OC⊥AB于点D,∠E=30°,连接OA.
(1)求OA的长;
(2)若AF是⊙O的另一条弦,且点O到AF的距离为![]() ,直接写出∠BAF的度数.
,直接写出∠BAF的度数.

参考答案:
【答案】(1)OA=4;(2)∠BAF的度数是75°或15°.
【解析】
试题分析:(1)根据垂径定理求出AD的长,根据圆周角定理求出∠AOD的度数,运用正弦的定义解答即可;
(2)作OH⊥AF于H,根据勾股定理和等腰直角三角形的性质求出∠OAF的度数,分情况计算即可.
试题解析:(1)∵OC⊥AB,AB=![]() ,∴AD=DB=
,∴AD=DB=![]() ,∵∠E=30°,
,∵∠E=30°,
∴∠AOD=60°,∠OAB=30°,∴OA=4;
(2)如图,作OH⊥AF于H,∵OA=4,OH=![]() ,∴∠OAF=45°,
,∴∠OAF=45°,
∴∠BAF=∠OAF+∠OAB=75°,
则∠BAF′=∠OAF′﹣∠OAB=15°,
∴∠BAF的度数是75°或15°.
-
科目: 来源: 题型:
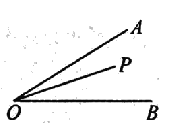
查看答案和解析>>【题目】如图,∠AOB=30°,内有一点P且OP=5,若M、N为边OA、OB上两动点,那么△PMN的周长最小为__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明用50元钱买笔记本和练习本共20本,已知每个笔记本5元,每个练习本1元,那么他最多能买笔记本本.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=x2+(2m﹣1)x+m2﹣1经过坐标原点,且当x<0时,y随x的增大而减小.
(1)求抛物线的解析式;
(2)结合图象写出,0<x<4时,直接写出y的取值范围 ;
(3)设点A是该抛物线上位于x轴下方的一个动点,过点A作x轴的平行线交抛物线于另一点D,再作AB⊥x轴于点B,DC⊥x轴于点C.当BC=1时,求出矩形ABCD的周长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组线段中,能构成三角形的是( )
A. 2,3,5 B. 3,4,5 C. 3,4,10 D. 2,5,8
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的两边长是6cm和3cm,那么它的周长是
A. 9cm B. 12 cm C. 12 cm或15 cm D. 15 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知两圆的半径分别是3和4,圆心距的长为1,则两圆的位置关系为( )
A.外离
B.相交
C.内切
D.外切
相关试题

