【题目】已知直线y=﹣ ![]() x+1与x轴、y轴分别交于B点、A点,直线y=2x﹣2与x轴、y轴分别交于D点、E点,两条直线交于点C;
x+1与x轴、y轴分别交于B点、A点,直线y=2x﹣2与x轴、y轴分别交于D点、E点,两条直线交于点C;
(1)求A、B、C、D、E的坐标;
(2)请用相似三角形的相关知识证明:AB⊥DE;
(3)求△CBD的外接圆的半径.
参考答案:
【答案】
(1)
解:在y=﹣ ![]() x+1中,令x=0可得y=1,令y=0可求得x=2,
x+1中,令x=0可得y=1,令y=0可求得x=2,
∴A(0,1),B(2,0),
在y=2x﹣2中,令x=0可得y=﹣2,令y=0可求得x=1,
∴D(1,0),E(0,﹣2),
联立两直线解析式可得 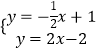 ,解得
,解得 ![]() ,
,
∴C( ![]() ,
, ![]() );
);
(2)
解:由(1)可知OA=1,OB=2,OD=1,OE=2,
∴ ![]() =
= ![]() ,且∠AOD=∠DOE,
,且∠AOD=∠DOE,
∴△AOB∽△DOE,
∴∠DEO=∠ABO,且∠ODE=∠CDB,
∴∠DCB=∠DOE=90°,
∴AB⊥DE;
(3)
解:由(2)可知∠DCB=90°,
∴BD为△CBD外接圆的直径,
∵OB=2,OD=1,
∴BD=1,
∴△CBD外接圆的半径为 ![]() .
.
【解析】(1)由两直线的解析式可求得A、B、D、E的坐标,再联立两直线解析式可求得C点坐标;(2)利用A、B、D、E的坐标可求得OA、OB、OD、OE的长,则可证得△AOB∽△DOE,可求得∠OED=∠OBA,则可求得∠DCB=90°,可证得结论;(3)由(2)的结论,结合圆周角定理可知BD即为△CBD的外接圆的直径,由B、D的坐标可求得BD的长,则可求得半径.
【考点精析】本题主要考查了一次函数的图象和性质和圆周角定理的相关知识点,需要掌握一次函数是直线,图像经过仨象限;正比例函数更简单,经过原点一直线;两个系数k与b,作用之大莫小看,k是斜率定夹角,b与Y轴来相见,k为正来右上斜,x增减y增减;k为负来左下展,变化规律正相反;k的绝对值越大,线离横轴就越远;顶点在圆心上的角叫做圆心角;顶点在圆周上,且它的两边分别与圆有另一个交点的角叫做圆周角;一条弧所对的圆周角等于它所对的圆心角的一半才能正确解答此题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在等腰Rt△ABC中,∠C=90°,AC=8,F是AB边上的中点,点D,E分别在AC、BC边上运动,且保持AD=CE,连接DE,DF,EF,在此运动过程中,下列结论:(1)△DFE是等腰直角三角形;(2)DE长度的最小值为4;(3)四边形CDFE的面积保持不变;(4)△CDE面积的最大值是4.正确的结论是( )

A. (1)(2)(3) B. (1)(3)(4) C. (1)(2)(4) D. (2)(3)(4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,AC=3,BC=4.分别以AB、AC、BC为边在AB的同侧作正方形ABEF、ACPQ、BDMC,四块阴影部分的面积分别为S1、S2、S3、S4.则S1+S2+S3+S4等于( )
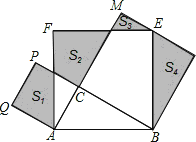
A.14 B.16 C.18 D.20
-
科目: 来源: 题型:
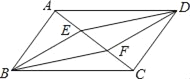
查看答案和解析>>【题目】如图,在□ABCD中,E,F是对角线AC上的两点且AE=CF,在①BE=DF;②BE∥DF;③AB=DE;④四边形EBFD为平行四边形;⑤S△ADE=S△ABE;⑥AF=CE这些结论中正确的是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形?并说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】手机微信推出了抢红包游戏,它有多种玩法,其中一种为“拼手气红包”,用户设定好总金额以及红包个数后,可以生成不等金额的红包.现有一用户发了三个“拼手气红包”,总金额为3元,随机被甲、乙、丙三人抢到.
(1)判断下列事件中,哪些是确定事件,哪些是不确定事件?
①丙抢到金额为1元的红包;
②乙抢到金额为4元的红包
③甲、乙两人抢到的红包金额之和一定比丙抢到的红包金额多;
(2)记金额最多、居中、最少的红包分别为A,B,C.
①求出甲抢到红包A的概率;
②若甲没抢到红包A,则乙能抢到红包A的概率又是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,在平面直角坐标系xoy中,抛物线y=(m﹣1)x2﹣(3m﹣4)x﹣3与x轴交于A、B两点,与y轴交于点C,抛物线的对称轴是经过(1,0)且与y轴平行的直线,点P是抛物线上的一点,点Q是y轴上一点;

(1)求抛物线的函数关系式;
(2)若以A、B、P、Q为顶点的四边形是平行四边形,求点P的坐标;
(3)若tan∠PCB= ,求点P的坐标.
,求点P的坐标.
相关试题

