【题目】下列条件中能判断△ABC为直角三角形的是( )
A.∠A +∠B = ∠CB.∠A = ∠B = ∠C
C.∠A-∠B = 90°D.∠A = ∠B = 3∠C
参考答案:
【答案】A
【解析】
根据各项的特点求出各角即可判断.
A. ∵∠A +∠B = ∠C,又∠A +∠B + ∠C=180°,
∴2∠C=180°
得∠C=90°,故为直角三角形;
B. ∠A = ∠B = ∠C, 又∠A +∠B + ∠C=180°,
∴∠A = ∠B = ∠C =60°故不是直角三角形;
C. ∠A-∠B = 90°,∠A +∠B + ∠C=180°,
不能得到∠A=90°,∠B = 90°,∠C=90°,
故不是直角三角形;
D. ∠A = ∠B = 3∠C,又∠A +∠B + ∠C=180°,
∴∠A = ∠B=![]() ×180°≠90°,∠C=
×180°≠90°,∠C=![]() ×180°≠90°,故不是直角三角形;
×180°≠90°,故不是直角三角形;
故选A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角尺画图:
(1)补全△A′B′C′
(2)画出AC边上的中线BD;
(3)画出AC边上的高线BE;
(4)求△ABD的面积 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】将若干个同样大小的小长方形纸片拼成如图形状的大长方形(小长方形纸片长为
 ,宽为
,宽为 ),请你仔细观察图形,解答下列问题:
),请你仔细观察图形,解答下列问题:(1)
 与
与 有怎样的关系?
有怎样的关系?(2)图中阴影部分的面积是大长方形面积的几分之几?
(3)请你仔细观察图中的一个阴影部分,根据它面积的不同表示方法写出含字母
 、
、 的一个等式.
的一个等式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
 经过
经过 ,
, 两点,抛物线与x轴的另一交点为A,连接AC、BC.
两点,抛物线与x轴的另一交点为A,连接AC、BC. 求抛物线的解析式及点A的坐标;
求抛物线的解析式及点A的坐标; 若点D是线段AC的中点,连接BD,在y轴上是否存一点E,使得
若点D是线段AC的中点,连接BD,在y轴上是否存一点E,使得 是以BD为斜边的直角三角形?若存在,求出点E的坐标,若不存在,说明理由;
是以BD为斜边的直角三角形?若存在,求出点E的坐标,若不存在,说明理由; 如图2,P为抛物线在第一象限内一动点,过P作
如图2,P为抛物线在第一象限内一动点,过P作 于Q,当PQ的长度最大时,在线段BC上找一点M使
于Q,当PQ的长度最大时,在线段BC上找一点M使 的值最小,求
的值最小,求 的最小值.
的最小值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,AE丄BD交BD的'延长线于点E, ∠ABC = 72°,∠C:∠ADB =2:3,求∠BAC 和∠DAE 的度数.
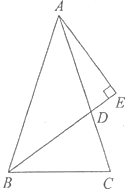
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长是13.
(1)如果腰长是底边长的
 ,求底边的长;
,求底边的长;(2)若该三角形其中两边的长为3x和2x+ 5,求底边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3cm,设运动的时间为t秒.
(1)当t= 时,CP把△ABC的周长分成相等的两部分?
(2)当t= 时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP的面积为18?

相关试题

