【题目】如图1,抛物线![]() 经过
经过![]() ,
,![]() 两点,抛物线与x轴的另一交点为A,连接AC、BC.
两点,抛物线与x轴的另一交点为A,连接AC、BC.
![]() 求抛物线的解析式及点A的坐标;
求抛物线的解析式及点A的坐标;
![]() 若点D是线段AC的中点,连接BD,在y轴上是否存一点E,使得
若点D是线段AC的中点,连接BD,在y轴上是否存一点E,使得![]() 是以BD为斜边的直角三角形?若存在,求出点E的坐标,若不存在,说明理由;
是以BD为斜边的直角三角形?若存在,求出点E的坐标,若不存在,说明理由;
![]() 如图2,P为抛物线在第一象限内一动点,过P作
如图2,P为抛物线在第一象限内一动点,过P作![]() 于Q,当PQ的长度最大时,在线段BC上找一点M使
于Q,当PQ的长度最大时,在线段BC上找一点M使![]() 的值最小,求
的值最小,求![]() 的最小值.
的最小值.


参考答案:
【答案】(1)![]() ;
;![]() 存在,
存在,![]() 或
或![]() ;
;![]() 的最小值是
的最小值是![]() .
.
【解析】
![]() 利用待定系数法求抛物线的解析式,令
利用待定系数法求抛物线的解析式,令![]() 解方程可得A的坐标;
解方程可得A的坐标;
![]() 根据
根据![]() ,构建辅助圆,与y轴有两个交点为点E,根据勾股定理列方程可得点E的坐标;
,构建辅助圆,与y轴有两个交点为点E,根据勾股定理列方程可得点E的坐标;
![]() 先作直线;
先作直线;![]() ,保证直线l与抛物线有一个公共点,即
,保证直线l与抛物线有一个公共点,即![]() ,可得P的坐标,过P作
,可得P的坐标,过P作![]() 轴,BC于M,此时
轴,BC于M,此时![]() 的值最小,根据三角函数求确定其最小值是PN的长即可.
的值最小,根据三角函数求确定其最小值是PN的长即可.
解:![]() 把
把![]() ,
,![]() 代入抛物线
代入抛物线![]() 中得:
中得:
 ,解得:
,解得:![]() ,
,
![]() 抛物线的解析式为:
抛物线的解析式为:![]() ,
,
当![]() 时,
时,![]() ,
,
解得:![]() ,
,![]() ,
,
![]() ;
;
![]() 存在,如图1,
存在,如图1,

![]() ,
,![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,
即![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() 或
或![]() ;
;
![]() ,
,![]() ,
,
易得BC的解析式为:![]() ,
,
如图2,作直线![]() ,
,

设直线l的解析式为:![]() ,
,
当直线l与抛物线有一个公共点时,这个公共点为P,此时PQ的长最大,
则![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
解得:![]() ,
,
![]() ,
,
过P作![]() 轴于N,交BC于M,
轴于N,交BC于M,
![]() ,
,
![]() ,
,
![]() ,
,
即![]() 的最小值是
的最小值是![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校英语社团举行了“单词听写大赛”,每位参赛选手共听写单词100个
 现从参加比赛的男女选手中分别随机抽取部分学生进行调查,对答对的情况进行分组如下:组:
现从参加比赛的男女选手中分别随机抽取部分学生进行调查,对答对的情况进行分组如下:组: ,B组:
,B组: ,C组:
,C组: ,D组:
,D组: ,E组:
,E组: 并绘制了如下不完整的统计图:
并绘制了如下不完整的统计图:
请根据以上信息解答下列问题:
 本次调查共抽取了多少名学生,并将条形统计图补充完整;
本次调查共抽取了多少名学生,并将条形统计图补充完整; 求出A组所对的扇形圆心角的度数;
求出A组所对的扇形圆心角的度数; 若从D、E两组中分别抽取一位学生进行采访,请用画树状图或列表法求出恰好抽到两位女学生的概率.
若从D、E两组中分别抽取一位学生进行采访,请用画树状图或列表法求出恰好抽到两位女学生的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在方格纸内将△ABC经过一次平移后得到△A′B′C′,图中标出了点B的对应点B′.根据下列条件,利用网格点和三角尺画图:
(1)补全△A′B′C′
(2)画出AC边上的中线BD;
(3)画出AC边上的高线BE;
(4)求△ABD的面积 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】将若干个同样大小的小长方形纸片拼成如图形状的大长方形(小长方形纸片长为
 ,宽为
,宽为 ),请你仔细观察图形,解答下列问题:
),请你仔细观察图形,解答下列问题:(1)
 与
与 有怎样的关系?
有怎样的关系?(2)图中阴影部分的面积是大长方形面积的几分之几?
(3)请你仔细观察图中的一个阴影部分,根据它面积的不同表示方法写出含字母
 、
、 的一个等式.
的一个等式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中能判断△ABC为直角三角形的是( )
A.∠A +∠B = ∠CB.∠A = ∠B = ∠C
C.∠A-∠B = 90°D.∠A = ∠B = 3∠C
-
科目: 来源: 题型:
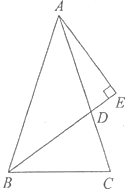
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,AE丄BD交BD的'延长线于点E, ∠ABC = 72°,∠C:∠ADB =2:3,求∠BAC 和∠DAE 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长是13.
(1)如果腰长是底边长的
 ,求底边的长;
,求底边的长;(2)若该三角形其中两边的长为3x和2x+ 5,求底边的长.
相关试题

