搜索
【题目】已知等腰三角形的周长是13.
（1）如果腰长是底边长的
，求底边的长；
（2）若该三角形其中两边的长为3x和2x+ 5,求底边的长.
参考答案：
【答案】（1）5（2）
【解析】
（1）设底边长＝a，则腰长＝
a，代入求出即可；
（2）已知条件中，没有明确说明已知的边长是否是腰长，所以需分情况讨论，还应判定能否组成三角形．
（1）解：设底边长＝a，则腰长＝a，
∵等腰三角形的周长是13.
∴a＋a＋a＝13，
解得a=5
∴底边的长为5；
（2）①3x=2x+5，解得x=5,腰长为15，不符合题意；
②3x+3x+2x+5=13，解得x=1,则三边分别为3,3,7，不能组成三角形；
③3x+2x+5+2x+5=13，解得x=
,则三边分别为,
,；
∴底边为
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，抛物线
经过
，
两点，抛物线与x轴的另一交点为A，连接AC、BC．
求抛物线的解析式及点A的坐标；
若点D是线段AC的中点，连接BD，在y轴上是否存一点E，使得
是以BD为斜边的直角三角形？若存在，求出点E的坐标，若不存在，说明理由；
如图2，P为抛物线在第一象限内一动点，过P作
于Q，当PQ的长度最大时，在线段BC上找一点M使
的值最小，求的最小值．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列条件中能判断△ABC为直角三角形的是（ ）
A.∠A +∠B = ∠CB.∠A = ∠B = ∠C
C.∠A-∠B = 90°D.∠A = ∠B = 3∠C
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，BD是△ABC的角平分线,AE丄BD交BD的'延长线于点E, ∠ABC = 72°，∠C：∠ADB =2：3,求∠BAC 和∠DAE 的度数.
-
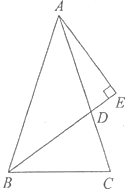
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC中，∠C＝90°，AC＝8cm，BC＝6cm，AB＝10cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒3cm，设运动的时间为t秒．
（1）当t＝ 时，CP把△ABC的周长分成相等的两部分？
（2）当t＝ 时，CP把△ABC的面积分成相等的两部分？
（3）当t为何值时，△BCP的面积为18？
-
科目： 来源： 题型：
查看答案和解析>>【题目】在一个不透明的袋里装有分别标有数字1，2，3，4，5的5个小球，除所有数字不同外，小球没有其他分别，每次试验前先搅拌均匀．
若从中任取一球，球上的数字为奇数的概率为多少？
若从中任取一球
不放回
，再从中任取1球，请用画树状图或列表的方法求出两个球上的数字之和为偶数的概率． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，四边形ABCD中，∠A = ∠B = 90°,AB边上有一点E,CE,DE分别是∠BCD和∠ADC 的角平分线，如果ABCD的面积是12,CD = 8,那么AB的长度为_____.
相关试题
