【题目】如图,△ABC中,∠C=90°,AC=8cm,BC=6cm,AB=10cm,若动点P从点C开始,按C→A→B→C的路径运动,且速度为每秒3cm,设运动的时间为t秒.
(1)当t= 时,CP把△ABC的周长分成相等的两部分?
(2)当t= 时,CP把△ABC的面积分成相等的两部分?
(3)当t为何值时,△BCP的面积为18?

参考答案:
【答案】(1)4;(2)![]() ;(3)当
;(3)当![]() 或
或![]() 时,
时,![]() 的面积为18.
的面积为18.
【解析】
(1)先根据CP把![]() 的周长分成相等的两部分可知,此时点P在边AB上,再根据线段的和差建立等式求解即可;
的周长分成相等的两部分可知,此时点P在边AB上,再根据线段的和差建立等式求解即可;
(2)先根据三角形的中线的性质确定点P的位置,从而可得AP的长,再根据线段的和差求出![]() 的长,由此即可得出答案;
的长,由此即可得出答案;
(3)分点P在边AC上和点P在边AB上两种情况,然后分别利用三角形的面积公式列出等式求解即可.
(1)由题意可知,只有当点P在边AB上,CP才能把![]() 的周长分成相等的两部分
的周长分成相等的两部分
则![]()
![]() 点P的运动速度为每秒
点P的运动速度为每秒![]()
![]()
![]()
![]()
则有![]()
解得![]()
即当![]() 时,CP把
时,CP把![]() 的周长分成相等的两部分
的周长分成相等的两部分
故答案为:4;
(2)当点P为AB中点时,由三角形的中线性质可知,此时![]() ,即CP把
,即CP把![]() 的面积分成相等的两部分
的面积分成相等的两部分
则![]()
由![]() 得:
得:![]()
解得![]()
故答案为:![]() ;
;
(3)点P运动至点A所需时间为![]() 秒,点P运动至点B所需时间为
秒,点P运动至点B所需时间为![]() (秒)
(秒)
由题意,分以下两种情况:
①当点P在边AC上,即![]() 时
时
![]()
则![]() ,即
,即![]()
解得![]() ,符合题设
,符合题设
②当点P在边AB上,即![]() 时
时
由(1)可知,![]()
如图,过点C作![]() 于点D
于点D
由![]() 的面积得:
的面积得:![]() ,即
,即![]()
解得![]()
则![]() ,即
,即![]()
解得![]() ,符合题设
,符合题设
综上,当![]() 或
或![]() 时,
时,![]() 的面积为18.
的面积为18.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列条件中能判断△ABC为直角三角形的是( )
A.∠A +∠B = ∠CB.∠A = ∠B = ∠C
C.∠A-∠B = 90°D.∠A = ∠B = 3∠C
-
科目: 来源: 题型:
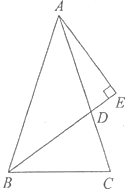
查看答案和解析>>【题目】如图,BD是△ABC的角平分线,AE丄BD交BD的'延长线于点E, ∠ABC = 72°,∠C:∠ADB =2:3,求∠BAC 和∠DAE 的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知等腰三角形的周长是13.
(1)如果腰长是底边长的
 ,求底边的长;
,求底边的长;(2)若该三角形其中两边的长为3x和2x+ 5,求底边的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋里装有分别标有数字1,2,3,4,5的5个小球,除所有数字不同外,小球没有其他分别,每次试验前先搅拌均匀.
 若从中任取一球,球上的数字为奇数的概率为多少?
若从中任取一球,球上的数字为奇数的概率为多少? 若从中任取一球
若从中任取一球 不放回
不放回 ,再从中任取1球,请用画树状图或列表的方法求出两个球上的数字之和为偶数的概率.
,再从中任取1球,请用画树状图或列表的方法求出两个球上的数字之和为偶数的概率. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD中,∠A = ∠B = 90°,AB边上有一点E,CE,DE分别是∠BCD和∠ADC 的角平分线,如果ABCD的面积是12,CD = 8,那么AB的长度为_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知甲、乙两地相距90km,A,B两人沿同一公路从甲地出发到乙地,A骑摩托车,B骑电动车,图中DE,OC分别表示A,B离开甲地的路程s(km)与时间t(h)的函数关系的图象,根据图象解答下列问题.
(1)A比B后出发几个小时?B的速度是多少?
(2)在B出发后几小时,两人相遇?

相关试题

