【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
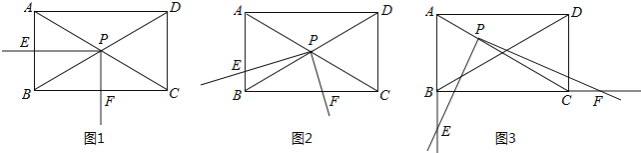
(1)当PE⊥AB,PF⊥BC时,如图1,则![]() 的值为 ;
的值为 ;
(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求![]() 的值;
的值;
(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,![]() 的值是否变化?证明你的结论.
的值是否变化?证明你的结论.
参考答案:
【答案】解:(1)![]() 。
。
(2)如答图1,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN。
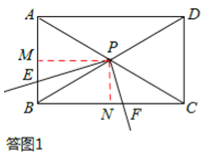
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
由(1)知,![]() ,
,
∴![]() 。
。
(3)变化。证明如下:
如答图2,过点P作PM⊥AB于点M,PN⊥BC于点N,则PM⊥PN,PM∥BC,PN∥AB。
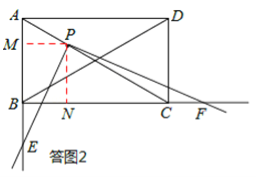
∵PM∥BC,PN∥AB,
∴∠APM=∠PCN,∠PAM=∠CPN。
∴△APM∽△PCN。
∴![]() ,得CN=2PM。
,得CN=2PM。
在Rt△PCN中,![]() ,
,
∴![]() 。
。
∵PM⊥PN,PE⊥PF,∴∠EPM=∠FPN。
又∵∠PME=∠PNF=90°,∴△PME∽△PNF。
∴![]() 。
。
∴![]() 的值发生变化
的值发生变化
【解析】
试题(1)证明△APE≌△PCF,得PE=CF;在Rt△PCF中,解直角三角形求得![]() 的值:
的值:
∵矩形ABCD,∴AB⊥BC,PA=PC。
∵PE⊥AB,BC⊥AB,∴PE∥BC。∴∠APE=∠PCF。
∵PF⊥BC,AB⊥BC,∴PF∥AB。∴∠PAE=∠CPF。
∵在△APE与△PCF中,∠PAE=∠CPF,PA=PC,∠APE=∠PCF,
∴△APE≌△PCF(ASA)。∴PE=CF。
在Rt△PCF中,![]() ,∴
,∴![]() 。
。
(2)如答图1所示,作辅助线,构造直角三角形,证明△PME∽△PNF,并利用(1)的结论,求得![]() 的值;
的值;
(3)如答图2所示,作辅助线,构造直角三角形,首先证明△APM∽△PCN,求得![]() ;然后证明△PME∽△PNF,从而由
;然后证明△PME∽△PNF,从而由![]() 求得
求得![]() 的值。与(1)(2)问相比较,
的值。与(1)(2)问相比较,![]() 的值发生了变化。
的值发生了变化。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线a,b,c表示三条公路,现要建一个货物中转站,要求它到三条公路的距离相等,则可供选择的地址有_________处。(填数字)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知a∥b,点A、B在直线a上,点C、D在直线b上,且AD⊥BC于E.
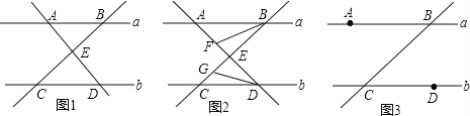
(1)求证:∠ABC+∠ADC=90°;
(2)如图2,BF平分∠ABC交AD于点F,DG平分∠ADC交BC于点G,求∠AFB+∠CGD的度数;
(3)如图3,P为线段AB上一点,I为线段BC上一点,连接PI,N为∠IPB的角平分线上一点,且∠NCD=
 ∠BCN,则∠CIP、∠IPN、∠CNP之间的数量关系是______.
∠BCN,则∠CIP、∠IPN、∠CNP之间的数量关系是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
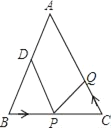
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A
 ,B
,B ,且满足
,且满足
(1)求A、B两点的坐标;
(2)点C
 在线段AB上,m、n满足n-m=5,点D在y轴负半轴上,连CD交x轴的负半轴于点M,且S△MBC=S△MOD,求点D的坐标;
在线段AB上,m、n满足n-m=5,点D在y轴负半轴上,连CD交x轴的负半轴于点M,且S△MBC=S△MOD,求点D的坐标;(3)平移直线AB,交x轴正半轴于E,交y轴于F,P为直线EF上第三象限内的点,过P作PG⊥x轴于G,若S△PAB=20,且GE=12,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(
 ),在四边形
),在四边形 中,
中, ,
, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 .探究图中线段
.探究图中线段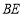 ,
, ,
, 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长 到点
到点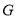 ,使
,使 ,连接
,连接 ,先证明
,先证明 ≌
≌ ,再证明
,再证明 ≌
≌ ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.如图(
 ),若在四边形
),若在四边形 中,
中, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.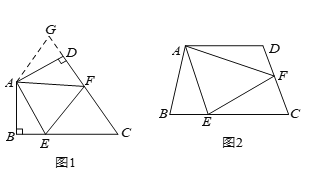
相关试题

