【题目】如图,已知△ABC中,AB=AC=10cm,BC=8cm,点D为AB的中点.如果点P在线段BC上以3cm/s的速度由点B向C点运动,同时,点Q在线段CA上由点C向A点运动.
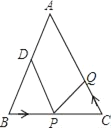
(1)若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPD与△CQP是否全等,请说明理由.
(2)若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPD与△CQP全等?
参考答案:
【答案】(1)详见解析;(2)点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为![]() cm/s时,能够使△BPD与△CQP全等.
cm/s时,能够使△BPD与△CQP全等.
【解析】
(1)经过1秒后,PB=3cm,PC=5cm,CQ=3cm,由已知可得BD=PC,BP=CQ,∠ABC=∠ACB,即据SAS可证得△BPD≌△CQP.
(2)可设点Q的运动速度为x(x≠3)cm/s,经过ts △BPD与△CQP全等,则可知PB=3t cm,PC=(8-3t)cm,CQ=xt cm,据(1)同理可得当BD=PC,BP=CQ或BD=CQ,BP=PC时两三角形全等,求x的解即可.
解:(1)经过1秒后,PB=3cm,PC=5cm, CQ=3cm,
∵△ABC中,AB=AC,
∴在△BPD和△CQP中,
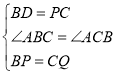 ,
,
∴△BPD≌△CQP(SAS).
(2)设点Q的运动速度为x(x≠3)cm/s,经过ts△BPD与△CQP全等;则可知PB=3t cm,PC=(8-3t)cm,CQ=xt cm,
∵AB=AC,
∴∠B=∠C,
根据全等三角形的判定定理SAS可知,有两种情况:
①当BD=PC,BP=CQ时,②当BD=CQ,BP=PC时,两三角形全等;
①当BD=PC且BP=CQ时,
8﹣3t=5且3t=xt,解得x=3,
∵x≠3,
∴舍去此情况;
②BD=CQ,BP=PC时,
5=xt且3t=8﹣3t,
解得:x=![]() ;
;
故若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为![]() cm/s时,能够使△BPD与△CQP全等.
cm/s时,能够使△BPD与△CQP全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,已知a∥b,点A、B在直线a上,点C、D在直线b上,且AD⊥BC于E.
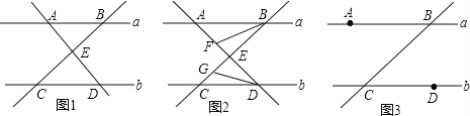
(1)求证:∠ABC+∠ADC=90°;
(2)如图2,BF平分∠ABC交AD于点F,DG平分∠ADC交BC于点G,求∠AFB+∠CGD的度数;
(3)如图3,P为线段AB上一点,I为线段BC上一点,连接PI,N为∠IPB的角平分线上一点,且∠NCD=
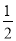 ∠BCN,则∠CIP、∠IPN、∠CNP之间的数量关系是______.
∠BCN,则∠CIP、∠IPN、∠CNP之间的数量关系是______. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某数学兴趣小组要测量一栋五层居民楼CD的高度,该楼底层为车库,高2.5米;上面五层居住,每层高度相等,测角仪支架离地1.5米,在A处测得五楼顶部点D的仰角为60°,在B处测得四楼顶部点E的仰角为30°,AB=14米,求居民楼的高度.(精确到0.1米,参考数据:
 ≈1.73)
≈1.73)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形ABCD中,∠ACB=30°,将一块直角三角板的直角顶点P放在两对角线AC,BD的交点处,以点P为旋转中心转动三角板,并保证三角板的两直角边分别于边AB,BC所在的直线相交,交点分别为E,F.
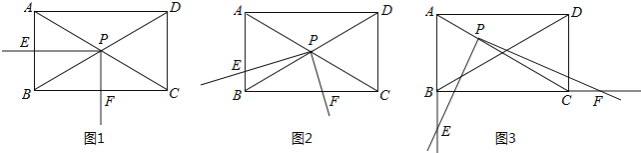
(1)当PE⊥AB,PF⊥BC时,如图1,则
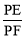 的值为 ;
的值为 ;(2)现将三角板绕点P逆时针旋转α(0°<α<60°)角,如图2,求
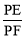 的值;
的值;(3)在(2)的基础上继续旋转,当60°<α<90°,且使AP:PC=1:2时,如图3,
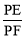 的值是否变化?证明你的结论.
的值是否变化?证明你的结论. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知A
 ,B
,B ,且满足
,且满足
(1)求A、B两点的坐标;
(2)点C
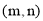 在线段AB上,m、n满足n-m=5,点D在y轴负半轴上,连CD交x轴的负半轴于点M,且S△MBC=S△MOD,求点D的坐标;
在线段AB上,m、n满足n-m=5,点D在y轴负半轴上,连CD交x轴的负半轴于点M,且S△MBC=S△MOD,求点D的坐标;(3)平移直线AB,交x轴正半轴于E,交y轴于F,P为直线EF上第三象限内的点,过P作PG⊥x轴于G,若S△PAB=20,且GE=12,求点P的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(
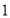 ),在四边形
),在四边形 中,
中, ,
, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 .探究图中线段
.探究图中线段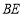 ,
, ,
, 之间的数量关系.小王同学探究此问题的方法是,延长
之间的数量关系.小王同学探究此问题的方法是,延长 到点
到点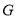 ,使
,使 ,连接
,连接 ,先证明
,先证明 ≌
≌ ,再证明
,再证明 ≌
≌ ,可得出结论,他的结论应该是__________.
,可得出结论,他的结论应该是__________.如图(
 ),若在四边形
),若在四边形 中,
中, ,
, ,
, ,
, 分别是
分别是 ,
, 上的点,且
上的点,且 ,上述结论是否仍然成立,并说明理由.
,上述结论是否仍然成立,并说明理由.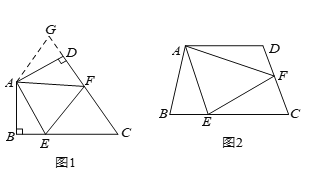
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一个长方体的三视图(单位:cm),根据图中数据计算这个长方体的体积是_______cm3.

相关试题

