【题目】如图,反比例函数![]() (
(![]() ,)的图象与直线
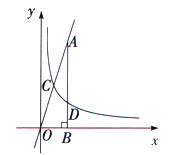
,)的图象与直线![]() 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
参考答案:
【答案】(1)1;(2)(![]() ,
, ![]() );(3) M(0,2
);(3) M(0,2![]() ﹣2).
﹣2).
【解析】(1)根据A坐标,以及AB=3BD求出D坐标,代入反比例解析式求出k的值;
(2)直线y=3x与反比例解析式联立方程组即可求出点C坐标;
(3)作C关于y轴的对称点C′,连接C′D交y轴于P,则P点即为所求,利用待定系数法求出直线C′D的解析式,进而可得出M点坐标.
解:A(1,3),
∴AB=3,OB=1,
∵AB=3BD,
∴BD=1,
∴D(1,1)
将D坐标代入反比例解析式得:k=1;
(2)由(1)知,k=1,
∴反比例函数的解析式为;y=![]() ,解:
,解:![]() ,
,
解得: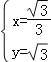 或
或 ,
,
∵x>0,
∴C(![]() ,
,![]() );
);
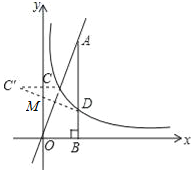
(3)如图,作C关于y轴的对称点C′,连接C′D交y轴于M,则d=MC+MD最小,
∴C′(﹣![]() ,
,![]() ),
), 
设直线C′D的解析式为:y=kx+b,
∴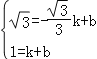 ,∴
,∴![]() ,
,
∴y=(﹣3+2![]() )x+2
)x+2![]() ﹣2,
﹣2,
当x=0时,y=2![]() ﹣2, ∴M(0,2
﹣2, ∴M(0,2![]() ﹣2).
﹣2).
“点睛”此题考查的是反比例函数综合题,涉及的知识有:坐标与图形性质,待定系数法确定函数解析式,以及直线与反比例的交点求法,熟练掌握待定系数法是解本题的关键.
-
科目: 来源: 题型:
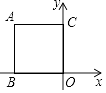
查看答案和解析>>【题目】如图,在平面直角坐标系中,正方形ABOC的顶点A在第二象限,顶点B在x轴上,顶点C在y轴上,若正方形ABOC的面积等于7,则点A的坐标是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.线段BF与图中现有的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.
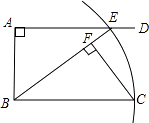
(1)结论:BF= .
(2)证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)解不等式3(x+2)﹣1≥5﹣2(x﹣2),并把解集在数轴上表示出来
(2)解不等式组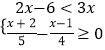 .
. -
科目: 来源: 题型:
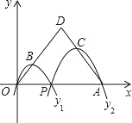
查看答案和解析>>【题目】如图,已知点A(6,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于______________。
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-kx-6=0的一个根为x=-3,则实数k的值为( )
A. 1B. -1C. 2D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2-3x+5=0的根的情况是( )
A. 有两个不相等的实根B. 有两个相等的实根C. 无实数根D. 不能确定
相关试题

