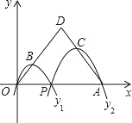
【题目】如图,已知点A(6,0),O为坐标原点,P是线段OA上任意一点(不含端点O,A),过P、O两点的二次函数y1和过P、A两点的二次函数y2的图象开口均向下,它们的顶点分别为B、C,射线OB与AC相交于点D.当OD=AD=5时,这两个二次函数的最大值之和等于______________。
参考答案:
【答案】4
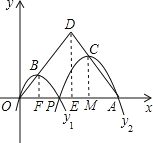
【解析】过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,则BF+CM是这两个二次函数的最大值之和,BF∥DE∥CM,求出AE=OE=2,DE=4,设P(3x,0),根据二次函数的对称性得出OF=PF=x,推出△OBF∽△ODE,△ACM∽△ADE,得出![]() ,
,![]() ,,代入求出BF和CM,相加即可求出答案.
,,代入求出BF和CM,相加即可求出答案.
解:过B作BF⊥OA于F,过D作DE⊥OA于E,过C作CM⊥OA于M,
∵BF⊥OA,DE⊥OA,CM⊥OA,
∴BF∥DE∥CM,
∵OD=AD=5,DE⊥OA,
∴OE=EA=![]() OA=3,
OA=3,
由勾股定理得:DE=![]() =4,
=4,
设P(3x,0),根据二次函数的对称性得出OF=PF=x,
∵BF∥DE∥CM,
∴△OBF∽△ODE,△ACM∽△ADE,
∴![]() ,
,![]() ,
,
∵AM=PM=![]() (OA-OP)=
(OA-OP)=![]() (6-2x)=3-x,
(6-2x)=3-x,
即![]() ,
,![]() ,
,
解得:BF=![]() ,CM=
,CM=![]()
∴BF+CM=![]() +
+![]() =4.
=4.
故答案为:4.
“点睛”此题考查了二次函数的最值,勾股定理,等腰三角形的性质,以及相似三角形的性质和判定的应用,题目比较好,但是有一定的难度,属于综合性试题.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD∥BC,∠BAD=90°,以点B为圆心,BC长为半径画弧,与射线AD相交于点E,连接BE,过C点作CF⊥BE,垂足为F.线段BF与图中现有的哪一条线段相等?先将你猜想出的结论填写在下面的横线上,然后再加以证明.
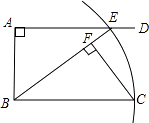
(1)结论:BF= .
(2)证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】综合题。
(1)解不等式3(x+2)﹣1≥5﹣2(x﹣2),并把解集在数轴上表示出来
(2)解不等式组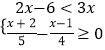 .
. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,反比例函数
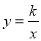 (
(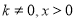 ,)的图象与直线
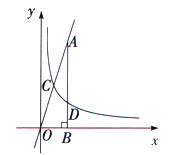
,)的图象与直线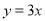 相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.
相交于点C,过直线上点A(1,3)作AB⊥x轴于点B,交反比例函数图象于点D,且AB=3BD.(1)求k的值;
(2)求点C的坐标;
(3)在y轴上确定一点M,使点M到C、D两点距离之和d=MC+MD最小,求点M的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的方程x2-kx-6=0的一个根为x=-3,则实数k的值为( )
A. 1B. -1C. 2D. -2
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程x2-3x+5=0的根的情况是( )
A. 有两个不相等的实根B. 有两个相等的实根C. 无实数根D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明袋子中装有2个红球,1个黄球,它们除颜色外其余都相同.小丽和小亮做摸球游戏,约定游戏规则是:小丽先从袋中任意摸出1个球记下颜色后不放回,小亮再从袋中摸出1个球记下颜色,如果两人摸到的球的颜色相同则小丽赢,否则小亮赢.
(1)请用树状图或列表格法表示一次游戏中所有可能出现的结果;
(2)这个游戏规则公平吗?请说明理由.
相关试题

