搜索
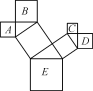
【题目】如图，图中所有的三角形都是直角三角形，四边形都是正方形，已知正方形A，B，C，D的边长分别是12，16，9，12，则最大正方形E的面积是_______.
参考答案：
【答案】625
【解析】
观察图形可知，M的面积是直角三角形斜边的平方，而直角三角形斜边的平方即为A的面积和B的面积之和，因此正方形A、B的面积和为正方形M的面积；同理，正方形C、D的面积和为正方形N的面积，正方形M、N的面积和为正方形E的面积，据此联系勾股定理即可求出E的面积.
根据勾股定理的几何意义可知，正方形A、B的面积和为正方形M的面积，
所以正方形M的面积为：122+162=400，
同理可得正方形N的面积为：92+122=225，
正方形E的面积为：400+225=625.
故答案为：625.
-
科目： 来源： 题型：
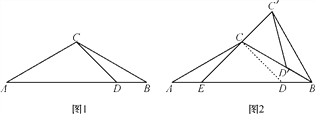
查看答案和解析>>【题目】如图1，△ABC中，AC＝BC，∠A＝30°，点D在AB边上，且∠ADC＝45°.
(1)求∠BCD的度数；
(2)将图1中的△BCD绕点B顺时针旋转得到△BC′D′，当点D′恰好落在BC边上时，如图2所示，连接C′C并延长交AB于点E.
①求∠C′CB的度数；
②求证：△C′BD′≌△CAE.
-
科目： 来源： 题型：
查看答案和解析>>【题目】阅读下面材料：
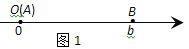
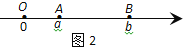
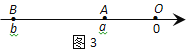
点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为∣AB∣.当A、B两点中有一点在原点时，不妨设点A在原点，如图1，∣AB∣＝∣OB∣＝∣b∣＝∣a-b∣；当A、B两点都不在原点时，如图2，点A、B都在原点的右边∣AB∣=∣OB∣-∣OA∣=∣b∣-∣a∣=
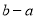=∣a-b∣；如图3，当点A、B都在原点的左边，∣AB∣＝∣OB∣-∣OA∣＝∣b∣-∣a∣=
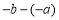=∣a-b∣；如图4，当点A、B在原点的两边，∣AB∣＝∣OB∣+∣OA∣＝∣a∣+∣b∣=
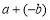=∣a-b∣.回答下列问题：
（1）数轴上表示2和5的两点之间的距离是_____，数轴上表示1和－3的两点之间的距离是______.
（2）数轴上若点A表示的数是x，点B表示的数是－2，则点A和B之间的距离是_____，若∣AB∣＝2，那么x为______.
（3）当x是_____时，代数式
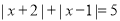.（4）若点A表示的数是-1，点B与点A的距离是10，且点B在点A的右侧，动点P、Q同时从A、B出发沿数轴正方向运动，点P的速度是每秒3个单位长度，点Q的速度是每秒
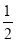个单位长度，求运动几秒后，点P与点Q之间的距离为5个单位长度 ？（请写出必要的求解过程） -
科目： 来源： 题型：
查看答案和解析>>【题目】小林同学积极参加体育锻炼,天天坚持跑步,他每天以1000m为标准,超过的记作正数,不足的记作负数.下表是一周内小明跑步情况的记录(单位：m)：
星期
一
二
三
四
五
六
日
跑步情况(m)
+420
+460
-100
-210
-330
+200
-240
(1)星期三小林跑了_____米
(2)小林在跑得最少的一天跑了______米?跑得最多的一天比最少的一天多跑了_____米?
(3)若小林跑步的平均速度为240米/分，求本周内小明用于跑步的时间.
-
科目： 来源： 题型：
查看答案和解析>>【题目】是某汽车行驶的路程S(km)与时间t(min)的函数关系图．观察图中所提供的信息，解答下列问题：
（1）汽车在前9分钟内的平均速度是多少？
（2）汽车在中途停了多长时间？
（3）当16≤t≤30时，求S与t的函数关系式．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某旅行社推出一条成本价位500元/人的省内旅游线路，游客人数y（人/月）与旅游报价x（元/人）之间的关系为y=﹣x+1300，已知：旅游主管部门规定该旅游线路报价在800元/人～1200元/人之间．
（1）要将该旅游线路每月游客人数控制在200人以内，求该旅游线路报价的取值范围；
（2）求经营这条旅游线路每月所需要的最低成本；
（3）档这条旅游线路的旅游报价为多少时，可获得最大利润？最大利润是多少？
【答案】（1）取值范围为1100元/人～1200元/人之间；（2）50000；（3）x=900时，w最大=160000
【解析】试题分析：（1）根据题意列不等式求解可；
（2）根据报价减去成本可得到函数的解析式，根据一次函数的图像求解即可；
（3）根据利润等于人次乘以价格即可得到函数的解析式，然后根据二次函数的最值求解即可.
试题解析：（1）∵由题意得
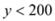时，即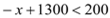
， ∴解得
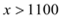
即要将该旅游线路每月游客人数控制在200人以内，该旅游线路报价的取值范围为1100元/人~1200元/人之间；
（2）
，
，∴
∵
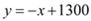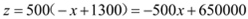
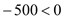，∴当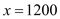
时，z最低，即
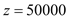；（3）利润
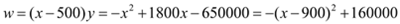
当
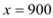时，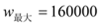
. 【题型】解答题
【结束】
23【题目】已知四边形ABCD中，AB=AD，对角线AC平分∠DAB，过点C作CE⊥AB于点E，点F为AB上一点，且EF=EB，连接DF．
（1）求证：CD=CF；
（2）连接DF，交AC于点G，求证：△DGC∽△ADC；
（3）若点H为线段DG上一点，连接AH，若∠ADC=2∠HAG，AD=3，DC=2，求
的值．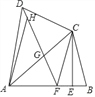
-
科目： 来源： 题型：
查看答案和解析>>【题目】观察下列两个等式：3+2=3×2-1，4+
＝4×-1，给出定义如下：我们称使等式a+b=ab-1成立的一对有理数a，b为“椒江有理数对”，记为（a，b），如：数对（3，2），（4，
）都是“椒江有理数对”．（1）数对（-2，1），（5，
）中是“椒江有理数对”的是 ；（2）若（a，3）是“椒江有理数对”，求a的值；
（3）若（m，n）是“椒江有理数对”，则（-n，-m） “椒江有理数对”（填“是”、“不是”或“不确定”）．
（4）请再写出一对符合条件的“椒江有理数对” （注意：不能与题目中已有的“椒江有理数对”重复）
相关试题
