【题目】对于实数a,我们规定:用符号[![]() ]表示不大于
]表示不大于![]() 的最大整数,称[
的最大整数,称[![]() ]为a的根整数,例如:[
]为a的根整数,例如:[![]() ]=3,[
]=3,[![]() ]=3.
]=3.
(1)仿照以上方法计算:[![]() ] = ;[
] = ;[![]() ] = .
] = .
(2)若[![]() ]=1,写出满足题意的x的整数值 .
]=1,写出满足题意的x的整数值 .
如果我们对a连续求根整数,直到结果为1为止.例如:对10连续求根整数2次 [![]() ]=3→[
]=3→[![]() ]=1,这时候结果为1.
]=1,这时候结果为1.
(3)对100连续求根整数, 次之后结果为1.
(4)只需进行3次连续求根整数运算后结果为1的所有正整数中,最大的是 .
参考答案:
【答案】(1)2,5;(2)1,2,3;(3)3;(4)最大的正整数是255,理由见解析
【解析】试题分析:(1)阅读上面的文件,仿照例子写出答案;
(2)根据题意,平方的数值范围,结合例子写出范围内的单即可;
(3)根据题意一次求出100的求根结果;
(4)由题意直接判断连续求根,确定最大数值即可.
试题解析:(1)∵22=4,52=25,62=36,
∴5<![]() <6,
<6,
∴![]() =[2]=2,[
=[2]=2,[![]() ]=5,
]=5,
故答案为:2,5;
(2)∵12=1,22=4,且![]() =1,
=1,
∴x=1,2,3,
故答案为:1,2,3;
(3)第一次:[![]() ]=10,
]=10,
第二次:[![]() ]=3,
]=3,
第三次:[![]() ]=1,
]=1,
故答案为:3;
(4)最大的正整数是255,
理由是:∵[![]() ]=15,[
]=15,[![]() ]=3,[
]=3,[![]() ]=1,
]=1,
∴对255只需进行3次操作后变为1,
∵[![]() ]=16,[
]=16,[![]() ]=4,[
]=4,[![]() ]=2,[
]=2,[![]() ]=1,
]=1,
∴对256只需进行4次操作后变为1,
∴只需进行3次操作后变为1的所有正整数中,最大的是255,
故答案为:255.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线y=
 x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
x+4与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
A.(﹣3,0)
B.(﹣6,0)
C.(﹣ ,0)
,0)
D.(﹣ ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线AB,CD 相交于点O,∠AOD=3∠BOD+20°.
(1)求∠BOD的度数;
(2)以O为端点引射线OE,OF ,射线OE平分∠BOD,且∠EOF= 90°,求∠BOF的度数.

-
科目: 来源: 题型:
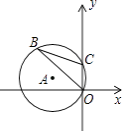
查看答案和解析>>【题目】如图,半径为3的⊙A经过原点O和点C(0,2),B是⊙O上一点,则tan∠OBC为 .
-
科目: 来源: 题型:
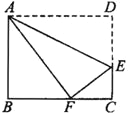
查看答案和解析>>【题目】如图所示,折叠长方形ABCD的一边AD,使点D落在BC边的点F处,已知AB=8cm,BC=10cm,求EF的长。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,AC=BC=
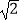 ,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= .
,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B,则C′B= . 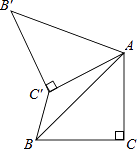
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形ABCD),经测量,在四边形ABCD中,AB=3m,BC=4m,CD=12m,DA=13m,∠B=90°.
(1)△ACD是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米100元,试问铺满这块空地共需花费多少元?

相关试题

