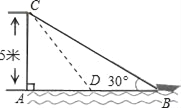
【题目】如图,在离水面高度为5m的岸上有人用绳子拉船靠岸,开始绳子与水面的夹角为30°,此人以每秒0.5m的速度收绳.
(1)8秒后船向岸边移动了多少米?
(2)写出还没收的绳子的长度S米与收绳时间t秒的函数关系式.

参考答案:
【答案】(1)![]() (m);(2)S=10﹣0.5t(0≤t≤10).
(m);(2)S=10﹣0.5t(0≤t≤10).
【解析】【试题分析】
(1)假设8秒后,船到达D位置,连接CD,
在Rt△ACB中,AC=5m,∠CBA=30°,根据30度所对的直角边是斜边的一半,得:CB=2AC=10m;此人以每秒0.5m的速度收绳,则8秒后收回的绳子长为:0.5×8=4m,
则CD=10﹣4=6(m);在Rt△ACD中,根据勾股定理得: AD=![]() (m);在Rt△ACB中,根据勾股定理得: AB=
(m);在Rt△ACB中,根据勾股定理得: AB=![]() (m),则BD=AB﹣AD=
(m),则BD=AB﹣AD=![]() (m);即8秒后船向岸边移动了
(m);即8秒后船向岸边移动了![]() 米.
米.
(2)原来绳子的长度为10米,以每秒0.5m的速度收绳,则t秒后剩下的绳长为(10-0.5t)米,即S=10﹣0.5t,由于绳长至少为5米,则要求0≤t≤10.
【试题解析】
(1)假设8秒后,船到达D位置,连接CD,
∵AC=5m,∠CBA=30°,
∴CB=2AC=10m,
此人以每秒0.5m的速度收绳,则8秒后收回的绳子长为:0.5×8=4m,
∴CD=10﹣4=6(m),
在Rt△ACD中: AD=![]() (m),
(m),
在Rt△ACB中:AB=![]() (m),
(m),
则BD=AB﹣AD=![]() (m);
(m);

(2)S=10﹣0.5t(0≤t≤10).
-
科目: 来源: 题型:
查看答案和解析>>【题目】古代丝绸之路上的花剌子模地区曾经诞生过一位伟大的数学家-“代数学之父”阿尔·花拉子米.在研究一元二次方程解法的过程中,他觉得“有必要用几何学方式来证明曾用数字解释过的问题的正确性”.

以
 为例,花拉子米的几何解法如下:
为例,花拉子米的几何解法如下:如图,在边长为
 的正方形的两个相邻边上作边长分别为
的正方形的两个相邻边上作边长分别为 和5的矩形,再补上一个边长为5的小正方形,最终把图形补成一个大正方形.
和5的矩形,再补上一个边长为5的小正方形,最终把图形补成一个大正方形.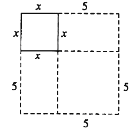
通过不同的方式来表达大正方形的面积,可以将原方程化为
 )2=39+ ,从而得到此方程的正根是 .
)2=39+ ,从而得到此方程的正根是 . -
科目: 来源: 题型:
查看答案和解析>>【题目】在△ABC中,若∠A=50°,∠B=55°,则△ABC是____________三角形;若∠A=50°,∠B=25°,则△ABC是____________三角形.(填“锐角”,“直角”或“钝角”)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系
 中,点
中,点 的坐标为(1,0),点
的坐标为(1,0),点 的横坐标为2,将点
的横坐标为2,将点  绕点P旋转,使它的对应点
绕点P旋转,使它的对应点 恰好落在
恰好落在 轴上(不与
轴上(不与 点重合);再将点
点重合);再将点 绕点O逆时针旋转90°得到点
绕点O逆时针旋转90°得到点 .
.(1)直接写出点
 和点C的坐标;
和点C的坐标;(2)求经过A,B,C三点的抛物线的表达式.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, 于
于 ,且
,且 .
.(
 )求证:
)求证: .
.(
 )若
)若 ,
, 于
于 ,
, 为
为 中点,
中点, 与
与 ,
, 分别交于点
分别交于点 ,
, .
.①判断线段
 与
与 相等吗?请说明理由.
相等吗?请说明理由.②求证:
 .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,将△ABC沿DE、EF翻折,顶点A,B均落在点O处,且EA与EB重合于线段EO,若∠CDO+∠CFO=108°,则∠C的度数为( )

A. 40° B. 41° C. 32° D. 36°
-
科目: 来源: 题型:
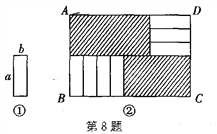
查看答案和解析>>【题目】将7张如图①所示的长为a、宽为b(a>b)的小长方形纸片,按如图②所示的方式不重叠地放在长方形ABCD内,未被覆盖的部分(两个长方形)用阴影表示,设左上角与右下角的阴影部分的面积之差为S,当BC的长度变化时,按照同样的放置方式,S始终保持不变,则a、b应满足( )
A. a=
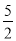 b B. a=3b C. a=
b B. a=3b C. a=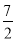 b D. a=4b
b D. a=4b
相关试题

