【题目】有三张正面分别标有数字:﹣1,1,2的卡片,它们除数字不同外其余全部相同,现将它们背面朝上,洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字.
(1)请用列表或画树形图的方法(只选其中一种),表示两次抽出卡片上的数字的所有结果;
(2)将第一次抽出的数字作为点的横坐标x,第二次抽出的数字作为点的纵坐标y,求点(x,y)落在双曲线上y= ![]() 上的概率.
上的概率.
参考答案:
【答案】
(1)解:根据题意画出树状图如下:
 ;
;
(2)解:当x=﹣1时,y= ![]() =﹣2,
=﹣2,
当x=1时,y= ![]() =2,
=2,
当x=2时,y= ![]() =1,
=1,
一共有9种等可能的情况,点(x,y)落在双曲线上y= ![]() 上的有2种情况,
上的有2种情况,
所以,P= ![]() .
.
【解析】(1)抓住已知洗匀后从中抽出一张记下数字,放回洗匀后再从中随机抽出一张记下数字,列出树状图即可求解。
(2)根据反比例函数图像上的点的坐标特点,k=xy,判断出在双曲线上的情况数,然后根据概率公式计算即可。
【考点精析】本题主要考查了列表法与树状图法和概率公式的相关知识点,需要掌握当一次试验要设计三个或更多的因素时,用列表法就不方便了,为了不重不漏地列出所有可能的结果,通常采用树状图法求概率;一般地,如果在一次试验中,有n种可能的结果,并且它们发生的可能性都相等,事件A包含其中的m中结果,那么事件A发生的概率为P(A)=m/n才能正确解答此题.
-
科目: 来源: 题型:
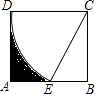
查看答案和解析>>【题目】如图,在矩形ABCD中,CD=2,以点C为圆心,CD长为半径画弧,交AB边于点E,且E为AB中点,则图中阴影部分的面积为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】班主任张老师为了了解学生课堂发言情况,对前一天本班男、女生发言次数进行了统计,并绘制成如下频数分布折线图(图1).

(1)请根据图1,回答下列问题:
①这个班共有名学生,发言次数是5次的男生有人、女生有人;
②男、女生发言次数的中位数分别是次和次;
(2)通过张老师的鼓励,第二天的发言次数比前一天明显增加,全班发言次数变化的人数的扇形统计图如图2所示,求第二天发言次数增加3次的学生人数和全班增加的发言总次数. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AD是△ABC的角平分线,DF⊥AB,垂足为F,DE=DG,△ADG和△AED的面积分别为48和36,求△EDF的面积________.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,直线MN交⊙O于A,B两点,AC是直径,AD平分∠CAM交⊙O于D,过D作DE⊥MN于E.

(1)求证:DE是⊙O的切线;
(2)若DE=6cm,AE=3cm,求⊙O的半径. -
科目: 来源: 题型:
查看答案和解析>>【题目】某服装厂生产一批男衬衫,经过抽样调查60名中年男子,得知所需衬衫型号的人数如表所示.求出它的中位数是74,众数是76,平均数是74.6,下列说法正确的是( )

A. 所需78号人数太少,78号的可以不生产
B. 这批衬衫可以一律按身长是74.6这个平均数生产
C. 因为众数是76,故76号的生产量要占第一位
D. 因为中位数是74,故74号的生产量要占第一位
-
科目: 来源: 题型:
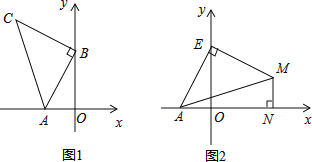
查看答案和解析>>【题目】如图1,
 ,
, ,以B点为直角顶点在第二象限作等腰直角
,以B点为直角顶点在第二象限作等腰直角 .
.
 求C点的坐标;
求C点的坐标; 在坐标平面内是否存在一点P,使
在坐标平面内是否存在一点P,使 与
与 全等?若存在,直接写出P点坐标,若不存在,请说明理由;
全等?若存在,直接写出P点坐标,若不存在,请说明理由; 如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角
如图2,点E为y轴正半轴上一动点,以E为直角顶点作等腰直角 ,过M作
,过M作 轴于N,直接写出
轴于N,直接写出 的值为 .
的值为 .
相关试题

